- #1
Xtensity
- 104
- 0
I haven't had calculus in over 2 years and so I am not exactly sure how to go about this. I am inclined to believe some form of integration would be needed.
I took the chart below from a paper on LED wavelength emission. The authors say that the vertical line represents the average emission wavelength. If say hypothetically I had a function to represent this graph, how would I go about finding this "average emission wavelength"? What is the process?
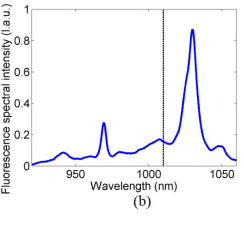
I took the chart below from a paper on LED wavelength emission. The authors say that the vertical line represents the average emission wavelength. If say hypothetically I had a function to represent this graph, how would I go about finding this "average emission wavelength"? What is the process?