How do I find the inertia tensor for a triangle with a given density function?

[Keplini]

Homework Statement

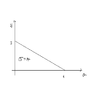
Find the center of mass and inertia tensor at the CoM of the following triangle. Density of the triangle is \sigma(x,y) = x and y=3-3/4x .

Homework Equations

Find the inertia tensor at the origin (x,y,z) and apply the parallel axis theorem

I_{ij}=\intdV(\delta^{ij}\vec{x}^{2}-x^{i}x^{j})

The Attempt at a Solution

I've been able to find the mass (which gave me 8 -correct me if I'm wrong-), the CoM and now I'm trying to find the inertia tensor. For the first component, I get something like:

I_{xx}=\int^{4}_{0}\int^{3-3/4x}_{0} xy^2 dx dy

which gives me something like

I_{xx}=\int^{4}_{0}x\frac{(3-3/4x^)^{3}}{3}dx

which looks like a big monster and I don't feel like integrating that ! ;) Basically, I believe it's getting way too complicated to be the good answer. Any help on finding that inertia tensor would be greatly appreciated !

Thanks,
Kep

 

[htown1397]

Hi, i need help on the same problem. So if anyone can help it would be great. By the way, Keplini, which book is this problem from?