Meadman23
- 43
- 0
Homework Statement
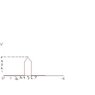
If I have a waveform that looks like it does in the attached picture, how can I figure out the y-int at the point where the line curves like triangle?
The Attempt at a Solution
This is confusing to me because I can figure out the slope of the triangle, but I don't see how there is a yint since the part of the form from x = 4 to x = 6 does not cross the y-axis.