How Do I Find the Y-int of a Curved Waveform?

[Meadman23]

Homework Statement

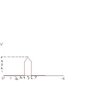
If I have a waveform that looks like it does in the attached picture, how can I figure out the y-int at the point where the line curves like triangle?

The Attempt at a Solution

This is confusing to me because I can figure out the slope of the triangle, but I don't see how there is a yint since the part of the form from x = 4 to x = 6 does not cross the y-axis.

 

[SteamKing]

Why do you want to find the y-intercept?

Are you sure you don't want to find y-max?

 

[Meadman23]

I figured that's the way I could solve for the function of this waveform.


That is, I could find the function of the part of the wave

1. from x = 0 to x = 4

2. from x = 4 to x = 5

3. from x = 5 to x = 6

Then, after I've deduced the correct functions that define each of the 3 parts of the waveform, I'd just add them up.

So, in my mind, since (2) is a slanted line, it must have an equation of the form y = mx+ b. m would simply be equal to [5-4]/[5-4] =1, but I don't see how I could get b.

 

[Mark44]

To get the equation of the part of the waveform between x = 4 and x = 5, use the slope you found (1) and a point on the line. One of these appears to be (4, 4).

The point-slope form of the equation of a line gives y - 4 = 1(x - 4), which simplifies to y = x.

The point-slope form is:

Given a line with slope m, that passes through the point (x₀, y₀), the equation of the line is

y - y₀ = m(x - x₀)

 

[Meadman23]

Okay, let me see if I get this right.

1. The slope of (1) is [4-0]/[4-0] = 1

2. Using this slope and the point (4,4) and plugging it into the y - y0 = m(x - x0) equation yields :

y - 4 = 1(x - 4) -> y - 4 = x -4 -> y = x

3. From this, my equation for (2) is then shown to be y = x?

 

[Mark44]

It's y = x for 4 ≤ x ≤ 5. The formula is valid on that interval. Other intervals have different formulas.