How Do I Solve Laser Reflection Using Vectors?

[sakkid95]

Question link: http://gyazo.com/4d52ab2521e5b222241718ea1b7ccb08.png
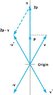
I have to solve this using vectors, not geometry

My professor said the equation that's required is -v* = 2 proj v onto n - v
and v* is reflected vector, so I don't really understand how to do this


First off I don't understand how to use the equation itself, our teacher hasn't done any examples, he just showed us how he derived the equation

My attempt
I found proj of v onto n for the first line was (0, x+a) x is first x value for mirror but I'm not really sure how I'm supposed to subtract the vector, and then I also don't understand how we're supposed to find cotangent in our solution.

If anyone could help explain what I'm supposed to do, I'd be very grateful, thanks.

 

[tiny-tim]

hi sakkid95!

I have to solve this using vectors, not geometry

i think he's expecting you to find the magnitude of 3[v - (v.n)n] by squaring it

 

[BvU]

Somewhat surprised no one came to your rescue ? Maybe you make it a little difficult to help you. You have seen the template, because your post does follow it somewhat.
I'll take the link as problem statement and will even venture to assume the coordinate system is such that the origin is at the source, x+ is to the right and y+ is upwards. Correct me if I am wrong.
So half the work is done when I see that the detector is sitting at y=a. For all t as far as I can see, but then: I have no idea what t is doing in this exercise!

I do wonder how you can let a $\cot \theta$ roll out of a vectors-only treatment, but we might get to that later on.

For 2. relevant equations -v* = 2 proj v onto n - v might do the trick, but I have to admit my english isn't up to translating that into either words or something mathematical that I can work out. Who is n ? Who is v ? Prof showed how he derived the equation. Did you understand what he meant? Can you rephrase or draw what you picked up from this showing ?

Now for

The Attempt at a Solution

, you adopt the same funny language as your teacher uses. Could you explain to me what it means and what it is intended to mean ? Because now I simply see a repetition of the given that the distance between the mirrors is a. This is because for x = 0 (as I daringly assmed) (0,x+a) is at the point (0,a).

Furthermore, from the context I can't deduce if this is an exercise in simple optics or a first step towards special relativity, or perhaps an introduction of vectors in a geometry course. Could you enlighten us ? My step 1 would be: calculate x at the point where the ray hits M1. Have you done that? What came out ?

(My long quick reply crossed Tim's)

 

[BvU]

OK, I have consulted a projontologist and he drew a few arrows on the blackboard (to do so he had to erase a few equations that looked like failures: [strike]E=ma²[/strike] [strike]E=mb²[/strike] ;-)

v is the first trajectory of your ray, from S to M1.
n is parallel to the normal to M1.
p is the newly learned projonton.
(Dashed line is v-p and its length is part of our x anwer!)
2p is twice p.
-v is just that: take v and put a - in front of each component (can only do that in a cartesian coordinate system!)
2p-v is start at the end of 2p and move by -v
Teacher has shown you end up at -v^*
do the minus thing and voila v^* !
Of course you want it to originate from the end of v, but that can be done easily: just shift it where you want it -- without changing size nor orientation.

Recognize any of this ? If not, ask or read up on it!
Now we are back to the question how you can let a cotθ roll out of a vectors-only treatment.
We know where θ is and we see something with x and a and θ. Is it OK to use that ?

Spoiler

The number 3 comes from reflecting twice. You can bring that in very easily by drawing the image S' of Source as M2 sees it reflected in M1 and then drawing the image S'' of S' as detector sees it reflected in M2. We still know where θ is and now we see something with x and 3a and θ.
I don't know how to include a picture in a spoiler and I'm pretty busy tomorrow, so you'll have to take a rain check for that.

 

[HalfLostAndSearching]

I would recommend seeking clarification from your professor on how to use the given equation for solving this problem. Understanding the derivation of the equation is important, but it is also crucial to know how to apply it in a practical situation.

That being said, here is a general overview of how the equation could be used to solve this problem:

1. Identify the incident vector (v) and the normal vector (n) of the mirror surface.
2. Use the equation -v* = 2 proj v onto n - v to calculate the reflected vector (v*).
3. Use the calculated reflected vector to determine the angle of reflection using the law of reflection (angle of incidence = angle of reflection).
4. Use the angle of reflection to calculate the cotangent, which is the ratio of the adjacent side to the opposite side of a right triangle formed by the incident and reflected vectors.
5. Repeat this process for each mirror the laser beam reflects off of, taking into account the angle of incidence and the normal vector for each mirror.
6. The final reflected vector will be the sum of all the calculated reflected vectors.
7. Use the final reflected vector to determine the direction and path of the laser beam after reflecting off of all the mirrors.

I hope this helps guide you in solving the problem using vectors. However, it is always best to seek clarification from your professor to ensure you are approaching the problem correctly.