How Do I Solve This Rotational Motion Problem?

Click For Summary

Homework Help Overview

The discussion revolves around a problem in rotational motion, specifically focusing on calculating moments around specific points in a given scenario. Participants are examining the setup and the forces involved.

Discussion Character

  • Exploratory, Assumption checking

Approaches and Questions Raised

  • Participants suggest calculating moments around points A or B and question the validity of using tan37° in the original poster's approach. There is a mention of considering additional forces that may have been overlooked.

Discussion Status

Some participants have provided guidance on how to approach the problem, and there is acknowledgment of a misunderstanding in the original calculations. The original poster indicates that they have resolved their confusion regarding the forces involved.

Contextual Notes

The original poster shared images of the problem and their attempts, which may contain specific details relevant to the calculations but are not fully described in the discussion.

coldblood
Messages
133
Reaction score
0
Hi friends,
Please help me in solving this problem, I'll appreciate the help.

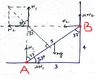
The problem is as:

https://fbcdn-sphotos-h-a.akamaihd.net/hphotos-ak-frc3/q71/s720x720/1390659_1461728134054292_1386292618_n.jpg


Attempt -

https://fbcdn-sphotos-c-a.akamaihd.net/hphotos-ak-ash3/q84/s720x720/1525033_1461728557387583_1961156759_n.jpg


Thank you all in advance.
 
Physics news on Phys.org
Try to calculate moment around point A or B. I don't think your equation tan37° is valid.
 

Attachments

  • Untitled.png
    Untitled.png
    26.9 KB · Views: 451
  • Like
Likes   Reactions: 1 person
mishek said:
Try to calculate moment around point A or B. I don't think your equation tan37° is valid.

Thanks dear, I got the answer. I was making the last equation in the wrong manner. I was only considering N1 ans N2 and forgot about the other forces which are acting there.
 
The problem has been cleared.
 

Similar threads

How Do You Solve This Rotational Motion Problem?
  • · Replies 13 ·
Replies
13
Views
3K
What is the Solution to this Rotational Motion Problem?
  • · Replies 7 ·
Replies
7
Views
2K
How Do I Solve This Rotational Motion Problem?
  • · Replies 2 ·
Replies
2
Views
2K
How to Solve This Rotational Motion Problem?
  • · Replies 5 ·
Replies
5
Views
2K
Rotational Motion: Solving a Problem with Translational and Angular Motion
  • · Replies 11 ·
Replies
11
Views
2K
What is the Solution to a Rotational Motion Problem?
  • · Replies 4 ·
Replies
4
Views
2K
What is the Moment of Inertia for a Rod?
  • · Replies 5 ·
Replies
5
Views
2K
How Can Vector Analysis Improve Understanding of Mechanics Problems?
  • · Replies 34 ·
2
Replies
34
Views
4K
How Do You Solve This Rotational Motion Problem?
  • · Replies 10 ·
Replies
10
Views
2K
Understanding Friction in Rotational Motion: Solving a Common Misconception
  • · Replies 26 ·
Replies
26
Views
3K