Handitya Alfa
- 1
- 0
Homework Statement
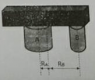
two cylinders A and B with the same initial length, standing upright with one another. Then on top of the cylinder is placed a rod horizontally as shown. If the known diameter and Young's modulus cylinder A is twice the diameter and Young's modulus cylinder B. Determine:
1. The amount of the mass ratio of a cylinder to hold the rod
2. The amount of mass perbanfingan cylinder B to hold the rod
3. If the distance of the center of mass of the rod to the center of mass of the cylinder A is Ra and mass center distance to the center of mass of the cylinder rod B is Rb, calculate the ratio Ra / Rb