blackbody
- 5
- 0
Hi,
I just want to verify that my thought process for these problems is valid, any help would be appreciated. (I have pictures attached for each problem for clarity)
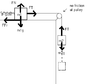
1) You have mass1 attached to a spring with a certain spring constant k, it rests on a tabletop with a force of friction with a coefficient \mu. Attached to mass1 is an ideal cord that extends over the table over an ideal pulley which holds mass2. a) If the spring is compressed a certain amount, and then released (spring stretches an amount x, smaller than max displacement), how far does mass2 move down? b) How much energy is dissipated by friction?
a) Ok, so I set my coordinate system as positive for mass1 to the right, and for mass2 positive is down. I'm assuming the accelerations for both blocks is equal?
For mass1 = \sum F_x = kx + F_T - \mu m_1g = m_1a
For mass2= \sum F_y = m_2g - F_T = m_2a
So I solve for a in both equations, set them equal to each other, and I get:
F_T = \frac{m_2(m_1g + \mu m_1g - kx)}{m_1 + m_2}
a = m_2(g - m_1g + \mu m_1g - kx)
Ok, times to stop for m_1 and m_2 are equal, but I don't know where to go from here.
b) I think I'm supposed to use the work energy theorem to figure out how much energy was dissipated by friction...but are the initial kinetic and potential energies of the system 0?
2) STATICS problem:
You have a uniform beam of length (l), mass M, supported by two wedges, Q and P. There are two boxes, W1 and W2 on top of the beam; each box has a different distance from the center of mass of the beam. a) What masses of W1 and W2 is the system stable? b) At which configuration does the normal force at Q goes to zero?
Ok, the second picture attached should help on the setup of the problem.
My solution:
Ok, so I need the \sum \tau around P to = 0, as well as the net force:
(counter-clockwise positive)
\sum \tau = W_1 A + Mg B - W_2 C - F_Q D = 0
\sum F = F_Q + F_P - W_1 - W_2 - Mg = 0
This is where I get stuck, and I'm not even sure these are right. Thanks for the help!
I just want to verify that my thought process for these problems is valid, any help would be appreciated. (I have pictures attached for each problem for clarity)
1) You have mass1 attached to a spring with a certain spring constant k, it rests on a tabletop with a force of friction with a coefficient \mu. Attached to mass1 is an ideal cord that extends over the table over an ideal pulley which holds mass2. a) If the spring is compressed a certain amount, and then released (spring stretches an amount x, smaller than max displacement), how far does mass2 move down? b) How much energy is dissipated by friction?
a) Ok, so I set my coordinate system as positive for mass1 to the right, and for mass2 positive is down. I'm assuming the accelerations for both blocks is equal?
For mass1 = \sum F_x = kx + F_T - \mu m_1g = m_1a
For mass2= \sum F_y = m_2g - F_T = m_2a
So I solve for a in both equations, set them equal to each other, and I get:
F_T = \frac{m_2(m_1g + \mu m_1g - kx)}{m_1 + m_2}
a = m_2(g - m_1g + \mu m_1g - kx)
Ok, times to stop for m_1 and m_2 are equal, but I don't know where to go from here.
b) I think I'm supposed to use the work energy theorem to figure out how much energy was dissipated by friction...but are the initial kinetic and potential energies of the system 0?
2) STATICS problem:
You have a uniform beam of length (l), mass M, supported by two wedges, Q and P. There are two boxes, W1 and W2 on top of the beam; each box has a different distance from the center of mass of the beam. a) What masses of W1 and W2 is the system stable? b) At which configuration does the normal force at Q goes to zero?
Ok, the second picture attached should help on the setup of the problem.
My solution:
Ok, so I need the \sum \tau around P to = 0, as well as the net force:
(counter-clockwise positive)
\sum \tau = W_1 A + Mg B - W_2 C - F_Q D = 0
\sum F = F_Q + F_P - W_1 - W_2 - Mg = 0
This is where I get stuck, and I'm not even sure these are right. Thanks for the help!
Attachments
Last edited: