rickportega
- 6
- 0
Homework Statement
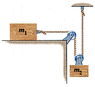
In the drawing, the rope and the pulleys are massless, and there is no friction. (m1 = 8.4 kg, and m2 = 2.95 kg.)
(a) Find the tension in the rope.
(b) Find the acceleration of the 8.4-kg block. (Hint: The larger mass moves twice as far as the smaller mass.)
Homework Equations
F=ma
The Attempt at a Solution
Im not familiar with how pulleys affect masses. I guessed that (m2*9.8) was the tension in the rope, which was wrong. Then I tried (m2*9.8)/2, figuring that the end attached to the ceiling takes 1/2 the force away. Is this reasoning wrong? It seems to make sense, but it was wrong too. For the acceleration, I tried (m2*9.8)/8.4, using the formula f=ma, but I think the f was wrong.
Question #2
Homework Statement
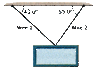
A 53.6 kg sign is suspended by two wires, as the drawing shows. Find the tension in wire 1 and in wire 2.
Homework Equations
F=ma
sin(x)=o/h
cos(x)=a/h
The Attempt at a Solution
I broke the two wire tensions into the components, saying that the two y components add up to equal (53.6*9.8), but I think that is where I went wrong. I then solved for the other sides of the "triangle" using (x/cos(55))+(x/cos(43)) = (53.6*9.8)
Even though the y components are the same length on paper, I guess the tensions are different. I am not really sure what else to try.
More details on attempt:
I solved for the components of each. What I got was for wire 1, the y component = T1cos(43) and the x component T1sin(43)
For wire 2, the y component = T2cos(55) and the x component = T2cos(55)
From this, I wrote two equations. T1+T2 = (9.8*53.6) = 525.28 and -(T1Sin(43))+(T2(Sin(55)) = 0, figuring that the addition of the x components should equal 0, since the wires come together at a point.
Using these 2 equations, I solved for T1 = 286.636 and T2 = 238.64
Attachments
Last edited: