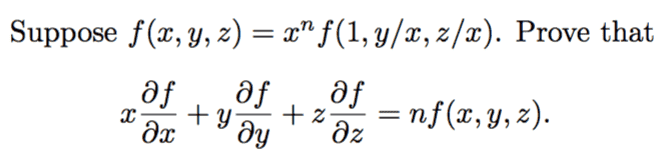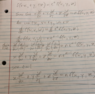dakota1234
- 3
- 1
Moved from a technical forum, so homework template missing
I've been working on this one for a little bit, and I know I really just need to use the chain rule to solve it, but I can't seem to figure out how to set it up properly. Probably a dumb question, but I could really use some help on this!