How Do You Calculate Angular Momentum for a Rotating Rigid Structure?

[shell4987]

Homework Statement

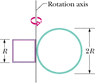
Figure 11-45 shows a rigid structure consisting of a circular hoop of radius R and mass m, and a square made of four thin bars, each of length R and mass m. The rigid structure rotates at a constant speed about a vertical axis, with a period of rotation of 2.8 s. Assuming R = 0.62 m and m = 1.2 kg, calculate (a) the structure's rotational inertia about the axis of rotation and (b) its angular momentum about that axis.

Homework Equations

I already solved part (a) but the equations to use for part (b) are L=Iw

The Attempt at a Solution

I put in the I that I received from part (a) which is 1.5, however I don't know how to find angular velocity... Can anyone help me out?

 

[hage567]

however I don't know how to find angular velocity... Can anyone help me out?

You figure it out from this:

The rigid structure rotates at a constant speed about a vertical axis, with a period of rotation of 2.8 s.