ttiger2k7
- 57
- 0
[PLEASE HELP!] Forces in members of a truss
A barrel vault truss is loaded as shown. Knowing that the length of the bottom chords DF, FH, ..., and QS is 3 ft, determine the force is members IK, JL, and JM.
http://img68.imageshack.us/img68/4817/fyjfhjfgjhfghgx8.jpg
Sum of y-components
\sum F_{x} = 0
x-components
\sum F_{y} = 0
Moment
\sum M = 0
First I did a free body diagram of the entire truss, which gave me three unknowns tosolve for first.
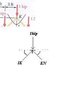
http://img392.imageshack.us/img392/9493/fyjfhjfgjhfgh1ur3.jpg
\sum F_{x} = 0:
A_{x} = 0
\sum F_{y} = 0:
A_{x} = (1+1.5+1.5+1+1.5+1.5+1) = A_{y} + V_{y}
9 kips = A_{y} + V_{y} ---- (1)
Solving for Moment about A
\sum M_{a} = 0:
V_{y} (18) = (1.5)(3) + (1.5)(6) + (1)(9) + (1.5)(12) + (1.5)(15) + (1)(18) =
V_{y} = 4.5 kips ----- (2)
Then plugging equation (2) into equation (1) I get
A_{y} = 4.5
Then I get stuck. I know I need to pass a section through the truss so I can get two portions, with each including the desired members I am solving for. Then I just draw a FBD and solve for no more than three unknowns.
Homework Statement
A barrel vault truss is loaded as shown. Knowing that the length of the bottom chords DF, FH, ..., and QS is 3 ft, determine the force is members IK, JL, and JM.
http://img68.imageshack.us/img68/4817/fyjfhjfgjhfghgx8.jpg
Homework Equations
Sum of y-components
\sum F_{x} = 0
x-components
\sum F_{y} = 0
Moment
\sum M = 0
The Attempt at a Solution
First I did a free body diagram of the entire truss, which gave me three unknowns tosolve for first.
http://img392.imageshack.us/img392/9493/fyjfhjfgjhfgh1ur3.jpg
\sum F_{x} = 0:
A_{x} = 0
\sum F_{y} = 0:
A_{x} = (1+1.5+1.5+1+1.5+1.5+1) = A_{y} + V_{y}
9 kips = A_{y} + V_{y} ---- (1)
Solving for Moment about A
\sum M_{a} = 0:
V_{y} (18) = (1.5)(3) + (1.5)(6) + (1)(9) + (1.5)(12) + (1.5)(15) + (1)(18) =
V_{y} = 4.5 kips ----- (2)
Then plugging equation (2) into equation (1) I get
A_{y} = 4.5
Then I get stuck. I know I need to pass a section through the truss so I can get two portions, with each including the desired members I am solving for. Then I just draw a FBD and solve for no more than three unknowns.
Last edited by a moderator: