How Do You Calculate Maximum Torsion in a Spring System?

[NicolaiTheDane]

I need to find the maximum contortion of a torsion spring, for a given system. Most of the assignment I have done correct, but this last part I simply cannot get right. The pictures below is what I have used, but they are probably not necessary for this problem.

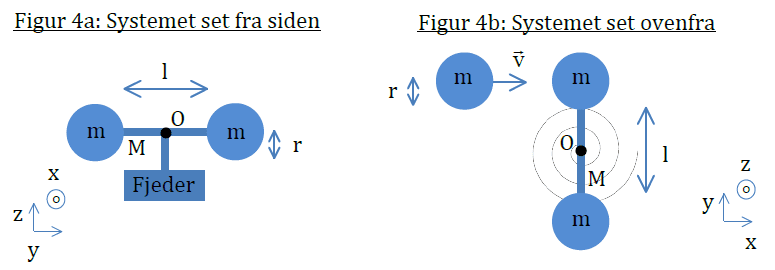
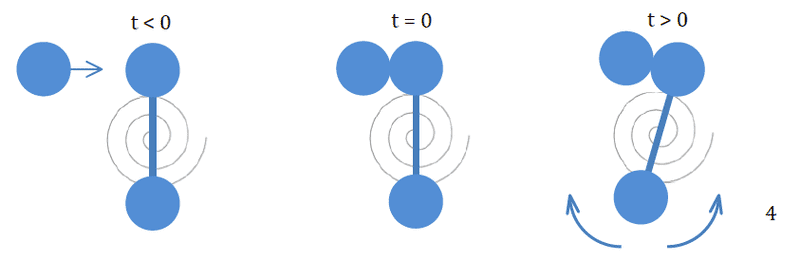
In prior parts of the problem, I figure out, that the angular momentum to the time 0, is

$L=-(l/2+r)*m*v$
Now the ways of writing the torque from the torsion spring, is as follows

$\tau = I*\alpha = -\kappa*\theta$

The attempt at a solution

My thought was, that to find an angular speed to a specific time, when knowing the time, the angular acceleration, and the angular speed at the start, I can use the following:

$\omega=\omega_0+\alpha*t$

I know that my angular momentum, to the specific time where the contortion is at its maximum is 0, as the spring has completely halted the rotational motion. I also know, that this happens at $t=T/4$, where $T$ is the period (or at least I assume that, as it would make sense thinking about the spring period). As multiplying the $I$ on all factors, gives us an equal that seems desirable, we do that, and get:

$$0=I*\omega_0+I*\alpha*t \Rightarrow 0=-(l/2+r)*m*v+(-\kappa*\theta)*(T/4)$$

From my physics book I also know that $T=2*\pi*\sqrt{\frac{I}{\kappa}}$. Plugging that in we get

$$0=I*\omega_0+I*\alpha*t \Rightarrow 0=-(l/2+r)*m*v-\frac{\kappa*\theta*\pi*\sqrt{\frac{I}{\kappa}}}{2}$$

Now the $\theta$ here, must to my understanding be the $\Theta$ I'm looking for, as that's that $\theta$ corresponding to the time I have plugged in. Solving for $\theta$ gives me:

$$\theta=\frac{2}{\pi}*\frac{(\frac{l}{2}+r)*m*v}{\sqrt{\kappa*I}}$$

Which according to the solution sheet is correct... except for that $\frac{2}{\pi}$.

I cannot see what I'm doing wrong, or what I have misunderstood. Please help.

 

[kuruman]

My thought was, that to find an angular speed to a specific time, when knowing the time, the angular acceleration, and the angular speed at the start, I can use the following:

$\omega=\omega_0+\alpha*t$

You cannot use that equation here. It applies to constant acceleration situations. Here the acceleration is not constant; it depends on the angle.

 

[NicolaiTheDane]

You cannot use that equation here. It applies to constant acceleration situations. Here the acceleration is not constant; it depends on the angle.

I suspected as much, but I have no idea on how to approach the problem then

 

[kuruman]

I assume that ω₀ is the angular speed of the combined three masses right after they are stuck together and just before the bar starts turning (θ = 0). If that's the case, then use energy conservation.

 

[NicolaiTheDane]

I assume that ω₀ is the angular speed of the combined three masses right after they are stuck together and just before the bar starts turning (θ = 0). If that's the case, then use energy conservation.

Using energy conservation doesn't work either.

Starting from $1/2*I*\omega^2=1/2*\kappa*\theta^2$ gets me the following

$$\theta^2=\frac{(\frac{l}{2}+r)*m*v}{\sqrt{\kappa*I}}$$

Its correct except its suppose to be $\theta$ and not $\theta^2$. Any ideas?

EDIT: It seems to work out now, though to say that I understand what is going on, is beyond a stretch

 

[kuruman]

Starting from $1/2 *I*\omega=1/2*\kappa*\theta^2$ gets me the following

Wrong starting point. The initial kinetic energy term is $K=\frac{1}{2}I \omega_0^2.$ Also, what is your expression for $\omega_0$ from the previous parts that you did not post?

 

[NicolaiTheDane]

Wrong starting point. The initial kinetic energy term is $K=\frac{1}{2}I \omega_0^2.$ Also, what is your expression for $\omega_0$ from the previous parts that you did not post?

Yea the omega not being squared was a mistake on my part. I assumed in my solution that my omega, comes as a result of the angular momentum. So I did the following
$$L=-\left(\frac{l}{2}+r\right)*m*v=I*\omega \Rightarrow \omega =\frac{-\left(\frac{l}{2}+r\right)*m*v}{I}$$
Plugging that in gives me
$$\frac{1}{2}*I*\frac{-\left(\frac{l}{2}+r\right)*m*v}{I}^2=\frac{1}{2}*\kappa*\theta^2$$
Solving for $\theta$ gives the following:
$$\theta=\frac{(\frac{l}{2}+r)*m*v}{\sqrt{\kappa*I}}$$
Which is the desired result. Like I said, I'm not entirely sure what I'm doing here

 

[kuruman]

Which is the desired result. Like I said, I'm not entirely sure what I'm doing here

This is what you are doing.

To find $\omega_0$ you need to conserve angular momentum before and after the collision. Linear momentum is not conserved because the two masses forming the dumbbell are presumably constrained from moving. Mechanical energy is not conserved because the collision is inelastic.

Right after the collision, mechanical energy is conserved. Initially all the mechanical energy is kinetic while at maximum angular displacement all the mechanical energy is potential. So you set the two equal to find the maximum angular displacement.

 

[NicolaiTheDane]

This is what you are doing.

To find $\omega_0$ you need to conserve angular momentum before and after the collision.

By this, I presume you mean I simply have to remember, that angular moment is conserved. Because that was I presumed, and just went with it. I didn't actually "do" anything :)

Anyway thanks a bunch for the help! I had already tried conservation of energy before you suggested it. But I forgot start after the collision, so my result was non-sense. I probably wouldn't have tried again, if you hadn't pointed it out. Out of curiosity. If you were to solve it, using calculus, how would you go about it?

 

[kuruman]

By this, I presume you mean I simply have to remember, that angular moment is conserved.

This is not something to remember but something to consider because angular momentum is not always conserved. What you should remember is that whenever you have a collision you need to consider not assume whether any of the following three quantities are conserved before and after the collision. These are
1. Linear momentum. This is conserved if there are no forces keeping any part of the system from moving in a straight line.
2. Angular momentum. This is conserved if there are no torques keeping the system from rotating about the reference axis.
3. Mechanical energy. This is conserved if there is language in the problem to indicate that it is. Such language may be, "neglect air resistance", "neglect friction", "the collision is elastic", etc. Specifically, for spring-mass systems the default assumption is that mechanical energy is conserved unless there is language to say that it is not. So if a problem said that a block is attached at the end of the spring and oscillates back and forth on a horizontal surface, you are to assume that the surface is frictionless otherwise the problem would have said the block oscillates on a rough surface. I know it's confusing, but people who construct problems often follow tacit conventions. So my advice to you is that before you apply any of the three conservation principles, put them to the test and use them only if they pass.

Any use of calculus for this problem would be contrived. There are no differential equations of motion to be solved and no rates of change to be calculated. However, you could change the problem and find the maximum torsional angle if κ were not constant, but depended on the angle. For example, what if κ = κ₀ + αθ, where κ₀ and α are constants?