How Do You Calculate R, L, and Tan θ in a Circuit with Sinusoidal Currents?

[MissP.25_5]

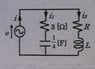
i1(t) = √2sin(2t+2π/3) [A]
i2(t) = √2sin(2t+π/6) [A]

1. Find R and L.
2. Given that the phase difference between e and i is arg(e/i)=θ. Find tan θ.I am not sure how to do this. I know that first we need to find e. Is it easier to use phasors to solve this or solve it in time function form? Did I get the e correct?

 

[rude man]

Too late tonite, someone else will probably chip in. Or me, 10 hrs later ...

BUT:
you can find e from i1(t) since R = 3 and C = 1/4F are given in the left branch (inner loop).
Then solve the outer loop for R and L, knowing e and i2(t).

Yes you should use phasors for e, i1 and i2, and complex forms of reactance. Using time-domain is messy but doable of course. Wouldn't try it myself.

 

[MissP.25_5]

Too late tonite, someone else will probably chip in. Or me, 10 hrs later ...

BUT:
you can find e from i1(t) since R = 3 and C = 1/4F are given in the left branch (inner loop).
Then solve the outer loop for R and L, knowing e and i2(t).

Yes you should use phasors for e, i1 and i2, and complex forms of reactance. Using time-domain is messy but doable of course. Wouldn't try it myself.

I will try to use phasors, then. But did get I the e(t) correct?

 

[rude man]

I will try to use phasors, then. But did get I the e(t) correct?

I don't know right off. Wouldn't express e that way.

Why not use phasors? E = phasor of e(t). Then

I1 = e^j2π/3
E = I1*Z
E, I1 and Z all complex. ω = 2.

 

[MissP.25_5]

I don't know right off. Wouldn't express e that way.

Why not use phasors? E = phasor of e(t). Then

I1 = e^j2π/3
E = I1*Z
E, I1 and Z all complex. ω = 2.

Can't we just take the magnitude of I1 and I2, without taking into account the phase? So that would be 1 amp for both I1 and I2. And here's what I have done so far, I got stuck in the end. It seems tedious too, I am sure there must be an easier way to do this but I just can't figure out.

 

[gneill]

Can't we just take the magnitude of I1 and I2, without taking into account the phase? So that would be 1 amp for both I1 and I2. And here's what I have done so far, I got stuck in the end. It seems tedious too, I am sure there must be an easier way to do this but I just can't figure out.

Nope. The phases are critical. The voltage source e is going to have phase, as will the total current, I.

When you have a phasor of the form $A e^{j \theta}$, you can write that as a complex number in polar or rectangular form. In polar form, A ∠ θ. You should be able to convert between polar and rectangular form as needed.

So, begin by determining the voltage source phasor E in complex form.

 

[MissP.25_5]

Nope. The phases are critical. The voltage source e is going to have phase, as will the total current, I.

When you have a phasor of the form $A e^{j \theta}$, you can write that as a complex number in polar or rectangular form. In polar form, A ∠ θ. You should be able to convert between polar and rectangular form as needed.

So, begin by determining the voltage source phasor E in complex form.

I did use phasors in the form of $A e^{j \theta}$ but still got the same result as the attached solution. What do you think of my working there?

 

[gneill]

I did use phasors in the form of $A e^{j \theta}$ but still got the same result as the attached solution. What do you think of my working there?

You dropped the angle and worked with magnitudes. That doesn't work; when complex numbers are multiplied or divided, the imaginary terms interact with the real terms.

Convert your current to rectangular form and then multiply by the rectangular form of the impedance.
The conversion is made easy because the angles involved have well known, exact values of sine and cosine.

 

[MissP.25_5]

You dropped the angle and worked with magnitudes. That doesn't work; when complex numbers are multiplied or divided, the imaginary terms interact with the real terms.

Convert your current to rectangular form and then multiply by the rectangular form of the impedance.
The conversion is made easy because the angles involved have well known, exact values of sine and cosine.

Rectangle form meaning x+yj form? And after I got the E, what should I do next?

 

[gneill]

Rectangle form meaning x+yj form?

Yup.

And after I got the E, what should I do next?

Well, you'll have the voltage E across and the current i2 through the unknown impedance...

 

[MissP.25_5]

Yup.

Well, you'll have the voltage E across and the current i2 through the unknown impedance...

So does that mean solving simultaneous equations? I mean, when we have E, we know that E is the same in each parallel and it's also the voltage for the whole circuit. The unknown impedance is R+j2L,right? That gives one equation E=(R+j2L)/(I2). And for the second equation, I'd find the total impedance of the circuit and get an equation E=Zs/(I1+I2). But this seems to be a really long work and takes time! Is there an easier way to get it?

 

[gneill]

So does that mean solving simultaneous equations? I mean, when we have E, we know that E is the same in each parallel and it's also the voltage for the whole circuit. The unknown impedance is R+j2L,right? That gives one equation E=(R+j2L)/(I2). And for the second equation, I'd find the total impedance of the circuit and get an equation E=Zs/(I1+I2). But this seems to be a really long work and takes time! Is there an easier way to get it?

Nothing nasty at all! Use Ohm's Law to find the complex value of the impedance of that branch. Equate terms.

 

[MissP.25_5]

Nothing nasty at all! Use Ohm's Law to find the complex value of the impedance of that branch. Equate terms.

Is this what you mean? I equate the real terms and imaginary terms, but the values seem unlikely, especially R, because I got it negative.

 

[MissP.25_5]

Is this what you mean? I equate the real terms and imaginary terms, but the values seem unlikely, especially R, because I got it negative.

Ok, I re-did it and got L=3 but I got R=2-3√3. Did I get them right? R is negative, though.

 

[gneill]

Is this what you mean? I equate the real terms and imaginary terms, but the values seem unlikely, especially R, because I got it negative.

Yeah, something's amiss with the real part of E; Overall the term should end up with a positive value. Better check that calculation.

 

[gneill]

Ok, I re-did it and got L=3 but I got R=2-3√3. Did I get them right? R is negative, though.

I'm seeing both terms of the impedance as simple integer values.

 

[gneill]

What is your final complex value for E?

 

[MissP.25_5]

Yeah, something's amiss with the real part of E; Overall the term should end up with a positive value. Better check that calculation.

Finally!Is this correct? L=3/2 and R=2.

 

[gneill]

Finally!Is this correct? L=3/2 and R=2.

Yes, that looks good. Huzzah!

 

[MissP.25_5]

Yes, that looks good. Huzzah!

Thanks! I still have to do the second question, finding tanθ.

 

[rude man]

Not to be a bore, but I would not convert to 'rectangular' form.

Work with my post #4. Compute E, then use that to get R and L.
What is E? (gneill's post # 17)?

 

[MissP.25_5]

Yes, that looks good. Huzzah!

Do I have to use rectangle form to find tanθ? I have to find arg(e/i). I tried and the calculation is really messy. Is there a faster way to do it?

 

[MissP.25_5]

Not to be a bore, but I would not convert to 'rectangular' form.

Work with my post #4. Compute E, then use that to get R and L.
What is E? (gneill's post # 17)?

How to calculate e^(j2∏/3) + e^(j∏/6) ?

 

[rude man]

How to calculate e^(j2∏/3) + e^(j∏/6) ?

I didn't realize this got posted, I wanted to leave all to gneill. I think sticking to polar form would just confuse you and on second thoughts I'm not at all sure that it's better than separating E, I1 and I2 into real and imaginary parts as gneill showed you.

In other words ... Never Mind! I'll keep tracking the thread to see how the rest of it turns out.

 

[MissP.25_5]

I didn't realize this got posted, I wanted to leave all to gneill. I think sticking to polar form would just confuse you and on second thoughts I'm not at all sure that it's better than separating E, I1 and I2 into real and imaginary parts as gneill showed you.

In other words ... Never Mind! I'll keep tracking the thread to see how the rest of it turns out.

Would you mind helping me with finding arg(e/i)? I don't what way is the best.

 

[gneill]

Would you mind helping me with finding arg(e/i)? I don't what way is the best.

Personally, I think I'd reach for a calculator at this point given the components of E !

However, if you can manage to slog through the complex math for E/I and separate out the real and imaginary parts, then you'll have your tan(θ)...

 

[rude man]

I deleted my last post since it was irrelevant.

OK, so you have solved for E. I would now express E in polar form: E = E₀exp(jθ₃). You don't need to compute E₀.

Next, I = I1 + I2. You need to do the addition rectangularly, you can't add polar quantities:
I1 = a + jb, I2 = c + jd and I1 + I2 = (a + c) + j(b + d) = I.

Now change I to polar: I = I₀exp(jθ₄), θ₄ = tan^-1[(b+d)/(a+c)]
& you don't need to compute I₀.

So now arg(E/I) = arg(E) - arg(I) = θ₃ - θ₄ = θ.

 

[MissP.25_5]

Personally, I think I'd reach for a calculator at this point given the components of E !

However, if you can manage to slog through the complex math for E/I and separate out the real and imaginary parts, then you'll have your tan(θ)...

But calculator is not used in my class and it's not allowed in exams. We don't need exact answers, we only need to calculate it to its simplest form as it can get.

 

[MissP.25_5]

I deleted my last post since it was irrelevant.

OK, so you have solved for E. I would now express E in polar form: E = E₀exp(jθ₃). You don't need to compute E₀.

Next, I = I1 + I2. You need to do the addition rectangularly, you can't add polar quantities:
I1 = a + jb, I2 = c + jd and I1 + I2 = (a + c) + j(b + d) = I.

Now change I to polar: I = I₀exp(jθ₄), θ₄ = tan^-1[(b+d)/(a+c)]
& you don't need to compute I₀.

So now arg(E/I) = arg(E) - arg(I) = θ₃ - θ₄ = θ.

Can you tell me what is E in its polar form? The numbers seem impossible, because it's out of the trigometry rules, I can't get the phase for E. Look at my working.

 

[rude man]

Can you tell me what is E in its polar form? The numbers seem impossible, because it's out of the trigometry rules, I can't get the phase for E. Look at my working.

You need to get comfortable moving between polar and rectangular forms of complex numbers.

OK, sermon over.

If E = a + jb, then E = sqrt(a^2 + b^2)exp(jθ) where θ = tan^-1b/a).

With what you're doing the coefficient sqrt(a^2 + b^2) is not important. The important quantity is exp(jθ).

Word of warning: keep track of the signs of a and b separately.
tan^-1(b/-a) is not the same phase angle as tan^-1(-b/a), for example.

 

[gneill]

But calculator is not used in my class and it's not allowed in exams. We don't need exact answers, we only need to calculate it to its simplest form as it can get.

I understand what you're saying. I've seen your rectangular form for E. I've seen your rectangular form for both I1 and I2, so I know that you can form I = I1 + I2.

Write out E/I and start simplifying. You might be surprised by how it (eventually) boils down to something tractable.

 

[MissP.25_5]

You need to get comfortable moving between polar and rectangular forms of complex numbers.

OK, sermon over.

If E = a + jb, then E = sqrt(a^2 + b^2)exp(jθ) where θ = tan^-1b/a).

With what you're doing the coefficient sqrt(a^2 + b^2) is not important. The important quantity is exp(jθ).

Word of warning: keep track of the signs of a and b separately.
tan^-1(b/-a) is not the same phase angle as tan^-1(-b/a), for example.

Yes, I know how to write E in its polar complex form, what i meant was for you to write it out for me just to see if it matches with mine. But I guess the easiest way is finding arg(E/I) instead of subtracting it separately because then you won't get tan theta. The only problem of solving E/I is separating its Re and I am part. Anyway, I did manage to find E/I and finally got the answer as tan theta= 1/5. Do you get the same answer as I do?

EDIT: i will attach my work later because I am using iphone now.

 

[MissP.25_5]

OK, so here's my final and complete work! I hope it is correct. Is it?

 

[gneill]

Yup. Good work!