Problems with currents and phase

[MissP.25_5]

I am still trying to solve this but I first, I need someone to explain to me about the sum of the currents, which I don't understand.

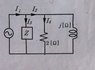
The phasor of current I1 is 2+3j[A], and the phasor of current I2 is 1[A].
1) Find the value of impedance Z.
2) Let the phase difference (arg(I3/I4)) between I3 and I4 be θ. Find the value of tan θ.

Ok, firstly, I am told that I1 = I2 + I3. My question is, what happened to I4?

 

[gneill]

I2 will split into I4 and whatever current continues on to the inductor (Maybe call it "I5", so that I2 = I4 + I5). Think of the segment labeled with I2 as a wire that connects to the parallel RL pair.

 

[MissP.25_5]

I2 will split into I4 and whatever current continues on to the inductor (Maybe call it "I5", so that I2 = I4 + I5). Think of the segment labeled with I2 as a wire that connects to the parallel RL pair.

Can you check if I got the impedance right, please?

 

[gneill]

Looks good! Be sure to include the units with the final value.

 

[MissP.25_5]

Looks good! Be sure to include the units with the final value.

Is this considered as a complete answer?

|Z| = (√50)/25 [Ω] , argZ = arctan(-1/7)

 

[gneill]

Is this considered as a complete answer?

|Z| = (√50)/25 [Ω] , argZ = arctan(-1/7)

The magnitude could be further reduced to √2 / 5. There's not much you can do with the arctan unless you resort to using a calculator.

 

[MissP.25_5]

The magnitude could be further reduced to √2 / 5. There's not much you can do with the arctan unless you resort to using a calculator.

So I guess, I could just leave the answer in its complex number form and put the unit Ω.
By the way, in the question it says that phase difference is arg(I3/I4), is it the same as arg(I3)-arg(I4)? I calculated both ways and got different answers, so it means they are different?

 

[gneill]

So I guess, I could just leave the answer in its complex number form and put the unit Ω.
By the way, in the question it says that phase difference is arg(I3/I4), is it the same as arg(I3)-arg(I4)? I calculated both ways and got different answers, so it means they are different?

The result should be the same. In polar form, when dividing one value by another you subtract the denominator's angle from the numerator's angle (and when you multiply, you add the angles).

 

[MissP.25_5]

Here is my solution, can you check please?

 

[MissP.25_5]

The result should be the same. In polar form, when dividing one value by another you subtract the denominator's angle from the numerator's angle (and when you multiply, you add the angles).

Oh, so it is like logarithm?

 

[gneill]

In your final line, if you take the arctan of both sides of the line above you should find that tan(θ) = 1/7. Otherwise, looks fine.

 

[MissP.25_5]

In your final line, if you take the arctan of both sides of the line above you should find that tan(θ) = 1/7. Otherwise, looks fine.

Oh yes, I got it:) Ok, so I tried to calculate argI3-argI4 and got tan^-1(3)-tan^-1(2). Is there a way to calculate that without calculator?

 

[gneill]

Oh, so it is like logarithm?

I suppose that it's similar, at least in a procedural way.

 

[MissP.25_5]

I suppose that it's similar, at least in a procedural way.

Yes, I meant the procedure. So question 2 is solved, then! Thanks again. I just posted a new question, hope you could help me out.

 

[gneill]

Oh yes, I got it:) Ok, so I tried to calculate argI3-argI4 and got tan^-1(3)-tan^-1(2). Is there a way to calculate that without calculator?

Offhand, I'm not sure; there may be a way via trig identities and/or geometry, but I'd have to give it some thought. Being essentially lazy, I tend to reach for a calculator