How Do You Calculate Resultant Forces in Ball and Wall Collision Scenarios?

[curiouschris]

Not a homework problem but pretty basic for you guys so I figure it belongs here

Two problems
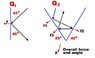
Q1

If I throw a steel ball (inelastic) at a wall at an angle of 45d how do I calculate the resultant force on the wall.

Q2

Extending question 1
I throw a steel ball at two steel plates welded together at 90 degrees. The ball hits one wall of the structure bounces off into the other wall and back to the original wall and then out again

How would I calculate the individual forces on the structure and then SUM them to calculate the overall resultant force on the structure.

I know this is a little unclear so I have included diagrams to show what I am looking for you may need to wait till the diagram is approved to see what I am looking for.

The problems seem fairly straightforward but my searches did not turn up a hit for the maths involved. I am probably not searching using the right criteria. My apologies in advance if this question has been answered multiple times before.CC

 

[jscushman]

If I throw a steel ball (inelastic) at a wall at an angle of 45d how do I calculate the resultant force on the wall.

You can't calculate the resultant force, but you can calculate the impulse. The impulse is the change in momentum, and assuming that this ball was traveling at velocity $$v$$ before the collision and was brought to a (horizontal) stop by the wall, the impulse would be $$\frac{mv}{\sqrt 2 }$$ (since the horizontal component of the initial velocity is $$v/\sqrt 2$$

 

[curiouschris]

Thanks jscushman. I am not sure what you mean by "brought to a (horizontal) stop" I think you mean all the energy was absorbed by the wall, is that correct? In the case above the ball bounces off the wall at its incident angle of 45 degrees, So I don't think your formula would apply would it? Or did you mean something else?

I found a very good and basic source of information, great for someone who has long forgotten his vector maths as I obviously have, hopefully it will help someone else
http://www.glenbrook.k12.il.us/gbssci/phys/Class/vectors/u3l1a.html

I still have a question but I am not sure it can be answered so I am continuing to look. that is how do I calculate how much momentum is lost when the steel ball hits the wall. I figure that will need to include material composition elasticity friction and probably gravity as well

So if anyone knows a good resource for that type of information it would be great. once I have the basic vector math I can then move to the next step in my problem modeling real world action.CC

 

[jscushman]

Thanks jscushman. I am not sure what you mean by "brought to a (horizontal) stop" I think you mean all the energy was absorbed by the wall, is that correct? In the case above the ball bounces off the wall at its incident angle of 45 degrees, So I don't think your formula would apply would it? Or did you mean something else?

I found a very good and basic source of information, great for someone who has long forgotten his vector maths as I obviously have, hopefully it will help someone else
http://www.glenbrook.k12.il.us/gbssci/phys/Class/vectors/u3l1a.html

I still have a question but I am not sure it can be answered so I am continuing to look. that is how do I calculate how much momentum is lost when the steel ball hits the wall. I figure that will need to include material composition elasticity friction and probably gravity as well

So if anyone knows a good resource for that type of information it would be great. once I have the basic vector math I can then move to the next step in my problem modeling real world action.


CC

Sorry! I misunderstood your original question. If the ball bounced off the wall, it wasn't an inelastic collision. Here's the updated explanation:

Assume that the ball is initially headed towards the wall with a speed v at an angle of 45˚. When it bounces off the wall, it will also be an an angle of 45˚. (Assuming that) the wall is vertical, and it can only provide a force normal to its surface, it can only change the horizontal velocity of the ball. In this case, the initial horizontal velocity is v/√(2) (which is from v cos 45˚), and the final horizontal velocity is -v/√(2), so the change in momentum (the mass times the change in velocity) is 2mv/√(2)=√(2) mv. The impulse is equal to the change in momentum.

To find the force that the ball applied to the wall you need to divide this impulse by the amount of time the ball was in contact with the wall.

 

[jscushman]

Extending question 1
I throw a steel ball at two steel plates welded together at 90 degrees. The ball hits one wall of the structure bounces off into the other wall and back to the original wall and then out again

How would I calculate the individual forces on the structure and then SUM them to calculate the overall resultant force on the structure.

This situation is impossible. After hitting one wall, it will hit the other wall, and then bounce back in the exact opposite direction as the initial velocity, parallel to the initial velocity. Draw an accurate picture (remember that the angle of incidence will equal the angle of reflection) and you'll see this for yourself. In this case, if the initial velocity is v, the final velocity will be -v, and the change in momentum (and therefore the impulse) will by 2mv. Hope this helps!