whynot314
- 76
- 0
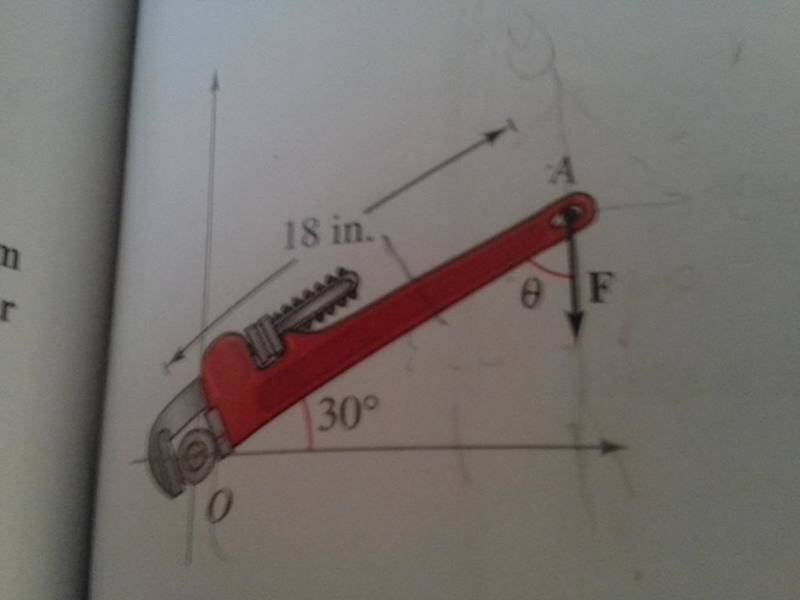
I just need help on 39 part a.
The answer to part a is 84sinθ
I first converted inches into feet.
I know how to set up the vector for the wrench which is simply OA= \frac{3\sqrt{3}}{4}i+\frac{3}{4}j
now as for the force vector I am kind of stuck because I know that Fsinθ is the only component to the force to cause rotation about O. so for F I get 0i and -56sinθ, when I do the cross product i get 42\sqrt{3}sinθ. I know i have the force part wrong I just can't see it.
[URL=http://s1341.photobucket.com/user/nebula-314/media/20130514_192552_zpsd6a49a82.jpg.html][PLAIN]http://i1341.photobucket.com/albums/o745/nebula-314/20130514_192552_zpsd6a49a82.jpg[/URL][/PLAIN]
 "]
"]
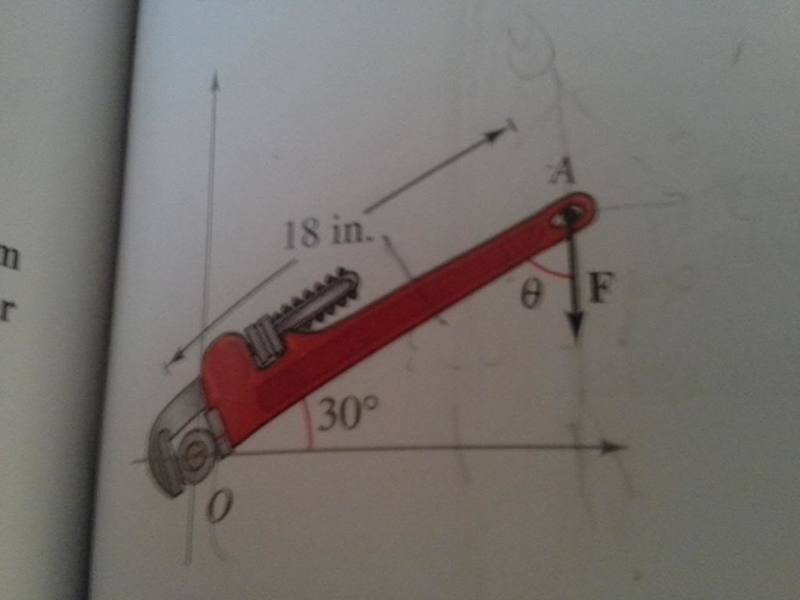
The answer to part a is 84sinθ
I first converted inches into feet.
I know how to set up the vector for the wrench which is simply OA= \frac{3\sqrt{3}}{4}i+\frac{3}{4}j
now as for the force vector I am kind of stuck because I know that Fsinθ is the only component to the force to cause rotation about O. so for F I get 0i and -56sinθ, when I do the cross product i get 42\sqrt{3}sinθ. I know i have the force part wrong I just can't see it.
[URL=http://s1341.photobucket.com/user/nebula-314/media/20130514_192552_zpsd6a49a82.jpg.html][PLAIN]http://i1341.photobucket.com/albums/o745/nebula-314/20130514_192552_zpsd6a49a82.jpg[/URL][/PLAIN]