How Do You Calculate the Electric Field at the Midpoint Between Two Charges?

[J89]

Homework Statement

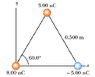
Three charges are at the corners of an equilateral triangle, as shown in the figure below. Calculate the electric field at a point midway between the two charges on the x-axis.

Magnitude:
Direction below the x-axis in degrees.

Homework Equations

F=Ke*q/(h)^2

The Attempt at a Solution

What I did 1st is since the charge 3.00 is in the midpoint..calculated .500sin60 to get .434
..then I just plugged it in the formula 8.99*10^9 * 3.00*10-6/(.434)^2 to get 144 N

for the two charges on the x axis..

I just divided the distance .500 by 2 to get .250 m and plugged in each charge seperately. I got 1.15*10^3 N and 719 N. Would you have to add them all up to get the total magnitude..and for the direction, I think you need to divide the two charges on the x-axis and take arc tan right? I'm not too sure, but I keep getting this wrong..someone please help.

 

[betel]

You have to remember that all quantities are vectors. So for the total magnitude you can only add the vectors.

Try sorting the numbers you got to the correct component of the Electric field vector.