mousesgr
- 31
- 0
Electricity and Magnetism urgent!pls!
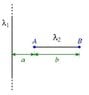
An infinite long line of charge of constant charge density a is located near the line AB which carries uniform charges with charge density b. Suppose both two lines are in the same plane, calculate the electrostatic force exerted on the line AB.
i don't know how to start...
An infinite long line of charge of constant charge density a is located near the line AB which carries uniform charges with charge density b. Suppose both two lines are in the same plane, calculate the electrostatic force exerted on the line AB.
i don't know how to start...
Last edited: