Addie
- 9
- 0
Analysis of a Moment! please help!
Please I tried for six hours to finish this seemingly easy problem yesterday I'm in dire need of help I've tried everything.
Heres the Problem:
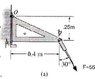
Q: For the loading condition shown below, determin the force on bolt O knowing that the triangular bracket is held up by the fixed shelf on the lower part of the wall.
(The value of F, is F=550 Newtons not 55 as it may appear in the picture.)
also I eventually found that the correct answer is F total=1037 N, but I don't know how to determine it.
Then found fx=275N and fy=-476 N from the componetns of f
What I did was Sum the Moments first take the moment of O and the Moment of A, since B cannot support a moment I didnt have one there.
so sum of M = M of o + M of A
sum of M's= 312.5 NM = (fay x .4 m) - (Foy x .4m)
and the
sum of x's=Fox=275
sum of y's=Foy=Ay-476
which makes the components of F, Fx= -275 and fy=681, which results no where near 1037 N...
I did somethign wrong I don't know what please help! thank you!
any help is much appreciated!
Please I tried for six hours to finish this seemingly easy problem yesterday I'm in dire need of help I've tried everything.
Heres the Problem:
Q: For the loading condition shown below, determin the force on bolt O knowing that the triangular bracket is held up by the fixed shelf on the lower part of the wall.
(The value of F, is F=550 Newtons not 55 as it may appear in the picture.)
also I eventually found that the correct answer is F total=1037 N, but I don't know how to determine it.
Then found fx=275N and fy=-476 N from the componetns of f
What I did was Sum the Moments first take the moment of O and the Moment of A, since B cannot support a moment I didnt have one there.
so sum of M = M of o + M of A
sum of M's= 312.5 NM = (fay x .4 m) - (Foy x .4m)
and the
sum of x's=Fox=275
sum of y's=Foy=Ay-476
which makes the components of F, Fx= -275 and fy=681, which results no where near 1037 N...
I did somethign wrong I don't know what please help! thank you!
any help is much appreciated!