How Do You Calculate the Magnetic Field Above a Current-Carrying Loop?

[skrat]

Homework Statement

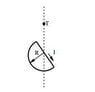
Calculate the magnetic field above a loop shown in picture with radius $R$ and current $I$.

Homework Equations

The Attempt at a Solution

Firstly, curved part:

$\vec{H}(\vec{r})=\frac{I}{4\pi }\int \frac{d\vec{{r}'}\times (\vec{r}-\vec{{r}'})}{|\vec{r}-\vec{{r}'}|^3}cos\varphi =\frac{I}{4\pi }\int \frac{Rd\varphi \hat{e}_{\varphi }\times (\vec{r}-\vec{{r}'})}{(R^2+z^2)^{3/2}}\frac{R}{\sqrt{R^2+z^2}}$

Where $\hat{e}_{\varphi }\times (\vec{r}-\vec{{r}'})=|\hat{e}_{\varphi }||\vec{r}-\vec{{r}'}|sin\varphi \hat{n}=\sqrt{R^2+z^2}\hat{n}$ and finally:

$\vec{H}(\vec{r})=\frac{I}{4\pi }\int_{\pi }^{2\pi }\frac{R^2\hat{n}d\varphi }{(R^2+z^2)^{3/2}}=\frac{IR^2}{4(R^2+z^2)^{3/2}}\hat{n}$.

For the straight line I have some troubles with the integral...

$\vec{H}(\vec{r})=\frac{I}{4\pi }\int \frac{d\vec{{r}'}\times (\vec{r}-\vec{{r}'})}{|\vec{r}-\vec{{r}'}|^3}$

Now $d\vec{{r}'}\times (\vec{r}-\vec{{r}'})=d\vec{{r}'}\times \vec{r}$ since $d\vec{{r}'}$ and $\vec{{r}'}$ are parallel. Also $d\vec{{r}'}=dx\hat{e}_x$.

$\vec{H}(\vec{r})=\frac{I}{4\pi }\int_{-R}^{R}\frac{dx(\hat{e}_x\times \vec{r})}{((\vec{r}-\hat{e}_xx)(\vec{r}-\hat{e}_xx))^{3/2}}=\frac{I(\hat{e}_x\times \vec{r})}{4\pi }\int_{-R}^{R}\frac{dx}{(r^2-2\hat{e}_x\vec{r} x+x^2)^{3/2}}$

Now what? Is this even ok?

 

[Simon Bridge]

Presumably you've already done it, or seen it done, for an infinite straight wire?

 

[skrat]

Aha, ok, I see it now...

$\hat{e}_x\vec{r}=0$ since they are always perpendicular. (My question here: What if they werent?)

In that case, things simplify a lot and the integral over the straight line should be $\vec{H}(\vec{r})=\frac{IR}{2\pi r\sqrt{R^2+r^2}}\hat{e}_y$, where $\vec{r}$ is the distance from the center of the straight line to point $T$.

 

[Simon Bridge]

When you don't have easy symmetry, the calculation can get arbitrarily difficult.
In many cases the integral has to be solved numerically.

That is why you will only see simple geometries at this stage.
Also consider what happens to the field close to one corner of the D ;)