HMPARTICLE
- 95
- 0
Homework Statement
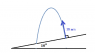
A catapult projects a stone in the normal direction to a playground which slopes at a angle of 10 degrees to the horizontal.
The initial speed of the stone is 18 m/s. calculate the range parallel to the playground.
Homework Equations
the usual ones!
The Attempt at a Solution
My first equation is v = 18cos10i + 18sin10j
using v = u + at in the y direction with a = -9.8m/s^2 and v = 0 u =18sin10
using this i find that the time that the stone hits the ground is t = 0.32 seconds
now in the x direction x = vt since we ignore air resistance
i obtain 18cos10(0.32) = 5. 8 m
the answer in the back of the book is 11.8 m.
so i am wrong. i think i have interpreted the question incorrectly!
but i have tried setting the angle to 80 degrees, but that came out horribly wrong