How Do You Calculate the X-Component of Electrical Force on a Charge?

[GingerBread27]

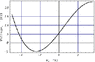
The electric potential along the x-axis (in kv) is plotted versus the value of x, (in meters). Evaluate the x-component of the electrical force (in Newtons)on a charge of 2.10 micro-C located on the x-axis at x=-3.6 m.

Ok I 'm doing Ex=-dV/dx. I get the slope to be (-7500 N/C) from doing -(5Kv-20kV)/(0m-2m). Then I am multiplying -7500N/C by the charge of 2.10 mC to get .01575 N and I need an answer in N so I thought this was right, and it's not lol. Help?

 

[MathStudent]

hmm... the graph isn't exactly linear in that interval, and those values don't look like they can be determined precisely just by looking at the graph ( no function is given for potential wrt x is there? ).
However checking your calculations, it looks like you multiplied -7500N/C by 2.10 micro coulombs (10^-6 C) . Micro has the symbol \mu
but in the problem, the charge is given in milli coulombs (10^-3 C ) so your answer might be off by a factor of 10^3.

 

[wais]

First, let's clarify a few things. The x-component of the electrical force is typically denoted as Fx, not Ex. Additionally, the slope of the electric potential graph is not the same as the electric field. The electric field is given by the negative of the derivative of electric potential with respect to distance, not position. So, we need to use the equation Fx = q * Ex, where q is the charge and Ex is the electric field.

To calculate the electric field at x=-3.6 m, we need to find the slope of the electric potential graph at that point. This can be done by finding the tangent line at x=-3.6 m. Using the slope formula, we get:

slope = (V2 - V1) / (x2 - x1) = (-7.5 kV - (-20 kV)) / (-1.8 m - (-2 m)) = 7500 N/C

Notice that we used -1.8 m instead of -3.6 m as the second x-value, since we are finding the slope at x=-3.6 m.

Now, we can calculate the x-component of the electrical force as:

Fx = (2.10 μC) * (7500 N/C) = 15.75 μN

Note that this answer is in micro-Newtons (μN), not Newtons (N). To convert to Newtons, we need to divide by 1 million, since 1 μN = 10^-6 N. So, the final answer is:

Fx = 15.75 μN / 1 million = 0.00001575 N

Therefore, the x-component of the electrical force on a charge of 2.10 μC located at x=-3.6 m is 0.00001575 N.