GRUMPYBLADE
- 5
- 0
Can anyone help?
I need a calculation to find the force required @ the shaft indicated, to achieve torque indicated at the locating faces.
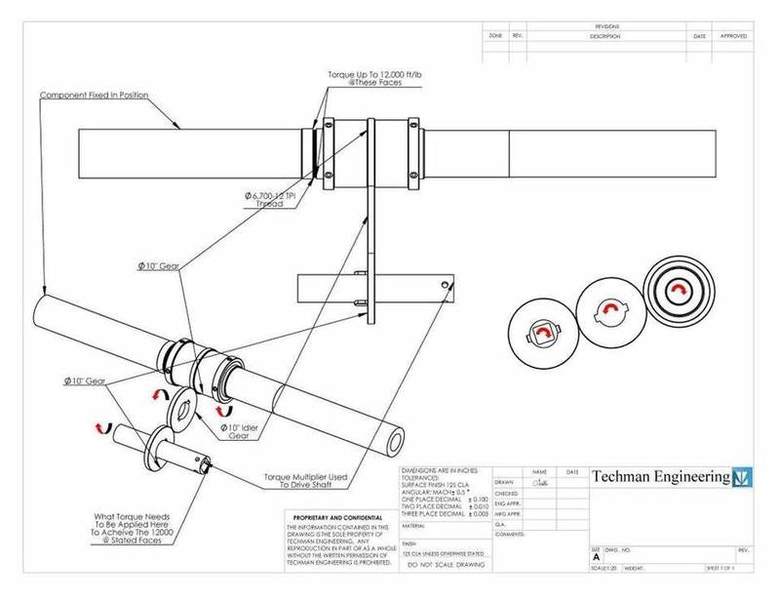 [/PLAIN]
[/PLAIN]
I need a calculation to find the force required @ the shaft indicated, to achieve torque indicated at the locating faces.