chadarebubble
- 3
- 0
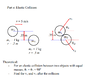
Homework Statement
The attached file is all the information on the problem
Homework Equations
.5mv^2 =.5mv1^2 + .5m2^2
p = mv
The Attempt at a Solution
I've tried plugging the known values in the equations and and substituting the various equations together and every time I come up with an equation that has two unknowns in it.