quality101
- 7
- 0
This is my first posting and I am a rookie at this so please bear with me. This is a General Physics I class w/trig.
I am having great difficulty understanding how to set up and solve a projectile motion problem. To further complicate things, my Physics instructor is showing us a method to solve for both position and velocity by manipulating the variables algebraically to simplify (she says) the problem into one variable prior to inserting any numbers.
I'll try to be as brief as I know how to show my work and where I am stuck as you suggest:
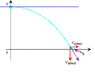
Problem: A stone is tossed horizontally off a 50.0 m cliff at a velocity of 18.0 m/s. a) How long does it take for the stone to strike the ground? b) With what speed and angle of impact does it land?
I have drawn 2 diagrams, one depicting the height of the cliff and the trajectory of the stone and the other a right angle triangle to determine the unknown angle and the unknown distance (x). I have chosen the coordinate system where x represents the ground and is positive and horizontal and y is positive up from the ground. We are not to consider any resistance upon the stone and we are considering the projectile motion from the time of release until just before it strikes the ground.
What I know (I think):
h = 50.0 m
vnaught = 18.0 m/s
(0,0) = intersection of vertical cliff and horizontal ground.
g = +9.80 m/s^2
t(inital) = 0
xnaught = 0
What I don't know:
angle (theta)
distance at final x(subf)
time at final t(subf)
vnaught(x)
vnaught(y)
I am attempting to solve for theta first and thus am using my second illustration. I know my vertical component y = 50.0 m and that is my Vnaught(y) and I know my hypotenuse Vnaught is 18.0 m/s. When trying to solve for Vnaught(x) using the pythagrean therom I am coming up with an entirely different answer than that given me in the book.
My approach: b^2 = c^2 - a^2
sqr b^2 = (sqr 18.0^2 - sqr 50.0^2)
sqr b^2 = (sqr 324 - sqr 2500)
sqr b^2 = (sqr -2176)
b = 46.6 m Vnaught(x) then = 46.6 m
Solving for theta: theta = tan(-1)(-46.6/50.0) = -42.98 deg.
The book's answer is -60.1 deg.
What am I missing?
I am having great difficulty understanding how to set up and solve a projectile motion problem. To further complicate things, my Physics instructor is showing us a method to solve for both position and velocity by manipulating the variables algebraically to simplify (she says) the problem into one variable prior to inserting any numbers.
I'll try to be as brief as I know how to show my work and where I am stuck as you suggest:
Problem: A stone is tossed horizontally off a 50.0 m cliff at a velocity of 18.0 m/s. a) How long does it take for the stone to strike the ground? b) With what speed and angle of impact does it land?
I have drawn 2 diagrams, one depicting the height of the cliff and the trajectory of the stone and the other a right angle triangle to determine the unknown angle and the unknown distance (x). I have chosen the coordinate system where x represents the ground and is positive and horizontal and y is positive up from the ground. We are not to consider any resistance upon the stone and we are considering the projectile motion from the time of release until just before it strikes the ground.
What I know (I think):
h = 50.0 m
vnaught = 18.0 m/s
(0,0) = intersection of vertical cliff and horizontal ground.
g = +9.80 m/s^2
t(inital) = 0
xnaught = 0
What I don't know:
angle (theta)
distance at final x(subf)
time at final t(subf)
vnaught(x)
vnaught(y)
I am attempting to solve for theta first and thus am using my second illustration. I know my vertical component y = 50.0 m and that is my Vnaught(y) and I know my hypotenuse Vnaught is 18.0 m/s. When trying to solve for Vnaught(x) using the pythagrean therom I am coming up with an entirely different answer than that given me in the book.
My approach: b^2 = c^2 - a^2
sqr b^2 = (sqr 18.0^2 - sqr 50.0^2)
sqr b^2 = (sqr 324 - sqr 2500)
sqr b^2 = (sqr -2176)
b = 46.6 m Vnaught(x) then = 46.6 m
Solving for theta: theta = tan(-1)(-46.6/50.0) = -42.98 deg.
The book's answer is -60.1 deg.
What am I missing?
Last edited: