How Does a Dielectric Wedge Affect Capacitor Performance?

[arnno]

Homework Statement

______|______
...
...
...
...
......
_____________
|


^ y
|
|_ _ > x

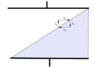
This is supposed to be a capacitor with a dielectric in a form of a wedge in it.
Known data: area A of the plates, permitivity $$\epsilon_r$$

The Attempt at a Solution

b is the depth of the capacity, l the length and d the space between the plates.
$$\frac{1}{dC}=\frac{1}{dC_1}+\frac{1}{dC_2}$$ $$=\frac{y}{\epsilon_0\epsilon_r dA}+\frac{d-y}{\epsilon_0 dA}$$ $$=\frac{1}{\epsilon_r\epsilon_0 dA} (y+\epsilon_r (d-y))$$ $$dC = \frac{dA \epsilon_r\epsilon_0}{(1-\epsilon_r)y+\epsilon_r d}$$$$=\frac{b\epsilon_r\epsilon_0 dx}{(1-\epsilon_r\frac{d}{l} x+\epsilon_r d)}$$
$$C=\frac{A\epsilon_r\epsilon_0}{(1-\epsilon_r)d} \ln(\frac{1}{\epsilon_r})$$
$$C=\frac{\epsilon_r\epsilon_0 A}{(\epsilon_r-1)d} \ln(\epsilon_r)$$

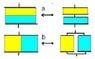
So I sliced the capacitor in thin parallel capacitors (so the slices orthogonal to the plates of the original capacitor). Those are again two capacitors, one with permitivity epsilon_r, one without.
But if I now slice the capacitor in thin capacitors parallel to the plates of the big capacitor, I get a different solution, which can't be the case.
Where is my fault?
Thanks in advance,
arnno

PS: sorry for my untrained english

 

[ehild]

Your derivation is correct, but slicing the capacitor parallel to its plates does not work, as the planes parallel to the plates are not equipotential surfaces.

ehild

 

[arnno]

Thanks for your answer.
I wanted to comprehend that.
I've drawn a better picture of it and included a closed path.
If I now go on that closed curve the total potential has to be zero as it would otherwise violate conservation of energy. So I get:
$$\oint_C \vec{E}\mathrm{d}\vec{s}=0$$ $$\int_{s_1} E^\perp _0 \mathrm{d} y -\int_{s_2}E^\perp _r \mathrm{d}y + \int_{s_3}E^\parallel _0 \mathrm{d}x-\int_{s_4}E^\parallel _r \mathrm{d}x=0$$
where E parallel is the electric field parallel to the plates and zero means outside the dielectric, the subscript r means inside the dielectric.
So with integral over the electric field equals the potential between beginning and end of the path I get:
$$U_{y,1}-U_{y,2}+U_{x,1}-U_{x,2}=0$$
So if, as you have said, the planes parallel to the plates are not on equal potential there must be an electric field parallel to the plates so that conservation of energy holds. But how is that possible? Where does it come from? Is it because the electric field is refracted at the transition of the dielectic to the non-dielectric?
Thanks in advance again
arnno

 

[TROGLIO]

this is an old sum of IIT JEE try and see the solution

the same sum is also there in H C VERMA
the solution of that book is available


you start
by cutting tha capacitor into smaller capacitors so thickness dx parallel to the plates of the capacitor
than take the slope of the dilectric as tan(theta)
and solve your integration from there
its a really fun sum to solve
i was very pleased with myself when i first did it

 

[ehild]

This is not all a simple problem. At the interface between two media, the parallel components of the electric field strength does not change but the normal components do : E2n/E1n=ε1/ε2, so the E lines "refract" at the interface. Even in case E was perpendicular to the plates in one medium, it would have an x component in the other one.

ehild

 

[tiny-tim]

i'm confused

don't these standard techniques assume that the charge is uniformly spread over each plate?

it isn't in this case, is it?

 

[ehild]

i'm confused

don't these standard techniques assume that the charge is uniformly spread over each plate?

it isn't in this case, is it?

The standard techniques apply in cases when the interface between the dielectrics is either parallel with the plates of the capacitor or normal to them (see picture).
In case a, the planar symmetry suggests that the equipotential surfaces are parallel to the plates, and both the electric field E and the electric displacement D are normal to the interface and uniform over the planes. As the normal component of the electric displacement D is the same at both sides of the interface, D is uniform over the whole capacitor. As the surface charge density is equal to D, the charge is uniformly spread over the plates. The interface is an equipotential surface, and can be substituted with a metal sheet, the capacitor is equivalent with two series connected ones.
In case b, the interface between the dielectrics is normal to the plates of the capacitor. The electric field can be considered normal to the plates because of symmetry. As the parallel components of the electric field are the same at both sides of an interface, E is the same at both dielectrics, E=U/d. The capacitor can be considered as two parallel connected ones, filled with different dielectrics.
The electric displacements are D₁=ε₁E and D₂=ε₁E, so the surface charge density is different at the parts of the capacitor filled with different dielectrics. If there is a stack of more dielectrics, the surface charge density is different over each one.

In both cases, the field lines all inside the dielectrics could be considered normal to the plates, which is not true for a wedge-shaped dielectric between the plates. So these standard methods do not apply, and I do not know, how the problem can be solved. What do you think, Tiny-Tim?

ehild

 

[tiny-tim]

hi ehild!

In both cases, the field lines all inside the dielectrics could be considered normal to the plates, which is not true for a wedge-shaped dielectric between the plates. So these standard methods do not apply, and I do not know, how the problem can be solved. What do you think, Tiny-Tim?

yes, i think you're right

i have no idea how to solve this problem …

i can't even visualise what either the E or D field lines would look like

 

[arnno]

I also tried it with gauß's law, but I'm stuck on that way, as I don't get an expression for the charge densities on the capacitor. Also it's quite hard to include the defraction, as the field line has to be normal to the transition of dielectric to vacuum because of symmetry (?) and therefore the lineintegral along the electric field gets complicated.
Really would like to know the correct sollution to the problem as well as how good the assumption is, that the field lines are parallel, as I did in my original solution.

But has the charge really have to be spread uniformly on the plates to solve the problem as I did in my first post? I assumed on that way, that on a capacitor with infinitessimal small plates the charge is constant, which in my opinion is ok, as D is constant in this infinitessimal capacitor. Then I sum up all those capacitors, which are parallel.
If I assume, that the field lines are normal to the plates all the time it's just the same (infinitessimal) as case b in ehilds post, where the charge is also not spread uniformly across the plates, as the E-field is constant along the x-axes, and therefore $$\frac{Q}{A}=D=E \epsilon_r \epsilon_0$$.
Btw: Thank you for taking so much interest in this problem :)
arnno

 

[tiny-tim]

hi arnno!

I assumed on that way, that on a capacitor with infinitessimal small plates the charge is constant, which in my opinion is ok, as D is constant in this infinitessimal capacitor. Then I sum up all those capacitors, which are parallel.
If I assume, that the field lines are normal to the plates all the time …

do you mean infinitesimal "vertical" plates?

then the edge-effects won't be negligible, and also I'm pretty sure the field lines aren't "vertical", so they simply don't go from one infinitesimal plate to the other

 

[arnno]

I mean infinitessimal plates parallel to the big plates of the capacitor.
To make it clearer, I've drawn it into my picture of the capacitor. It's also pointed out in my first post. As I seem to not be able to express properly what I mean, perhaps look at the math of my first post, it should get clearer then, I think.
arnno