How Does Double-Paned Glass Affect Heat Transfer?

[{~}]

1. Homework Statement [/b]

Consider a double-paned window consisting of two panes of glass, each with a thickness of 0.500 cm and an area of separated by a layer of air with a thickness of 1.75 cm. The temperature on one side of the window is 0.00 °C; the temperature on the other side is 20.0 °C. In addition, note that the thermal conductivity of glass is roughly 36 times greater than that of air. (a) Approximate the heat transfer through this window by ignoring the glass. That is, calculate the heat flow per second through 1.75 cm of air with a temperature difference of 20.0 C°. (The exact result for the complete window is 19.1 J/s.) (b) Use the approximate heat flow found in part (a) to find an approximate temperature difference across each pane of glass. (The exact result is 0.157 C°.) (Thermal conductivity of glass is 0.84 W/(m?K) and of air is 0.0234 W/(m?K))

2. Homework Equations [/b]

\frac{\Delta Q}{\Delta t} = kA\frac{T_{1} - T_{2}}{l}

3. The Attempt at a Solution [/b]

This is actually me trying to help someone else on another website and apparently failing

Here's what I got

Part (a)

Equation 19-16a from fourth edition Giancoli Physics for Scientist and Engineers

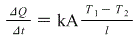
Our givens

k = 0.0234 W m-1 K-1

T1 - T2 = 20 K

l = 1.75x10-2 m

Leave the unknowns on the left side of the equation and substitute the givens on the right

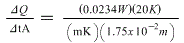
Note: The m K are part of the themal conductivity units

Evaluate

26.3 W m-2

Notice that this is not the complete answer for (a) because an area was not provided; however, this does not prevent me from completing (b)

Part (b)

I modify Eq 19-16a for a situation of series conduction

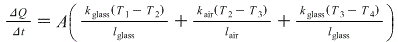
Substitute givens

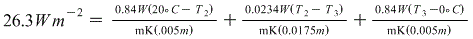
The algebra is a little intense but here goes

We have two unkowns but only one equation. We need another equation to solve the problem.

Lets draw a picture

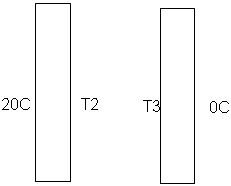
This problem has symetry that we can exploit

20C - T2 = T3 - 0C

T3 = 20C - T2 + 0C

Substitue and rearange

Note: I divided k and l for neatness

26.3 W m-2 = 168 W m-2 K-1 (20C - T2) + 1.34 W m-2 K-1 (T2 - (20C - T2 + 0C)) + 168 W m-2 K-1 ((20C - T2 + 0C) - 0C)
Simplify

26.3 K = 168 (40C - 2T2) + 1.34 (2T2 - 20C)

Distribute

26.3 K = 6720C - 336 T2 + 2.68 T2 - 26.8C

Evaluate

333 T2 = 6670 K

T2 = 20.0 C

Obviously I screwed up somehow I just can't see where

 

[ehild]

In case of series connection the current of heat is the same for each element, window-panes and air. Your equation for dQ/dt is wrong.

ehild