How Does Euler's Theorem Apply to Complex Eigenvalues in Differential Equations?

[FocusedWolf]

Ok, in my differential equation book, we're doing work on getting eigenvectors to complex eigenvalues.

anyway the author of the book only mentions Euler's Theorem as: http://rogercortesi.com/eqn/tempimagedir/eqn5095.png
and so he perfers to work with http://rogercortesi.com/eqn/tempimagedir/eqn7868.png when the roots are

So my question:

What is this called then?:

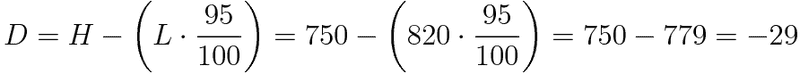
and can i use in place for

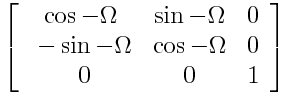and still call it Euler's Theorem?

 

[Dick]

It's called "Euler's theorem with -t substituted for t after applying the identity sin(-t)=-sin(t)". Does it really need a name?

 

[FocusedWolf]

Thx for that. I was sort of expecting some kind of identity to do that.