Picrill
- 2
- 0
Homework Statement
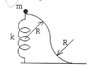
A particle of mass m is moving along a path composed by two two quarters of circumference of radius R (see attached picture). The spring acting on the particle has a known constant equal to k and an equilibrium length equal to R (the radius again). Due to friction, on the particle acts a constant force F. Find the speed of the particle when it gets on the table.
Homework Equations
Final speed of the particle?
The Attempt at a Solution
I would start by finding the total initial energy of the system, namely the potential energy stored in the spring plus the potential energy of the particle. The spring is compressed by mg/k so its energy is 1/2 (mg/k)^2. Therefore the mass energy is mg(R - mg/k). Summing this with some algebra I get:
E = 1/2 * (mg/k) * (2Rk - mg)
Then I have no idea how to use this. The kinetic energy theorem does not work, because there is friction, right? Anything?
Thanks!