rolodexx
- 14
- 0
[SOLVED] Partial Inelastic Collision
Is it ok if I keep this here for my own reference (and others if it helps them)? I don't know why it helps to type everything out before I realize what I did wrong! But looking back on my work seems to reinforce what I learned.
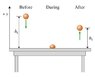
As shown in the figure (attached), a superball with mass m equal to 50 grams is dropped from a height of h_i = 1.5 m. It collides with a table, then bounces up to a height of h_f = 1.0 m. The duration of the collision (the time during which the superball is in contact with the table) is t_c = 15 ms. In this problem, take the positive y direction to be upward, and use g = 9.8m/s^2 for the magnitude of the acceleration due to gravity. Neglect air resistance.
The problem has 5 parts; with some logic and work I solved the fist 4, but the last one is really getting to me. It's weird, because it should be the easiest:
Find K_a - K_b, the change in the kinetic energy of the ball during the collision, in joules.
1 kg/1000 g
.5mv^2_a - .5mv^2_b
.5mv^2 = mgh (This was used for both v before and after)
Within the part of the problem I correctly solved were questions asking for the momentum immediately before and after the collision. Since p is solved for by multiplying mass and velocity, I used conservation of energy to relate gravitational potential energy (at h_i) to kinetic energy after the collision. I got a velocity v_b and multiplied it by the mass (.05 kg) to get a correct momentum for that part of the problem. The same logic was followed for the "after" momentum. The velocities I got from these two correct answers are what I used in this last question. (v_b=5.4 m/s; v_a=4.43 m/s)
I solved for the kinetic energies by multiplying .5 * .05kg * 19.6m^2/s^2 and .5 *.05kg * 29.4m^2/s^2. I then subtracted the "before" K (.729 J) by the "after" K (.491 J) to get .238 J.
But... it said "The ball bounces up to a lower height than that from which it was dropped. This implies that the kinetic energy after the collision was less than the kinetic energy before the collision." So I thought I had mixed up the two terms, and threw a negative sign in front of my answer, but that warranted a "Not quite. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures."
*edit* - It really was the wrong number of significant figure-rounding when calculating... that one is going to eat me forever if I don't stop it:shy:
Is it ok if I keep this here for my own reference (and others if it helps them)? I don't know why it helps to type everything out before I realize what I did wrong! But looking back on my work seems to reinforce what I learned.
Homework Statement
As shown in the figure (attached), a superball with mass m equal to 50 grams is dropped from a height of h_i = 1.5 m. It collides with a table, then bounces up to a height of h_f = 1.0 m. The duration of the collision (the time during which the superball is in contact with the table) is t_c = 15 ms. In this problem, take the positive y direction to be upward, and use g = 9.8m/s^2 for the magnitude of the acceleration due to gravity. Neglect air resistance.
The problem has 5 parts; with some logic and work I solved the fist 4, but the last one is really getting to me. It's weird, because it should be the easiest:
Find K_a - K_b, the change in the kinetic energy of the ball during the collision, in joules.
Homework Equations
1 kg/1000 g
.5mv^2_a - .5mv^2_b
.5mv^2 = mgh (This was used for both v before and after)
The Attempt at a Solution
Within the part of the problem I correctly solved were questions asking for the momentum immediately before and after the collision. Since p is solved for by multiplying mass and velocity, I used conservation of energy to relate gravitational potential energy (at h_i) to kinetic energy after the collision. I got a velocity v_b and multiplied it by the mass (.05 kg) to get a correct momentum for that part of the problem. The same logic was followed for the "after" momentum. The velocities I got from these two correct answers are what I used in this last question. (v_b=5.4 m/s; v_a=4.43 m/s)
I solved for the kinetic energies by multiplying .5 * .05kg * 19.6m^2/s^2 and .5 *.05kg * 29.4m^2/s^2. I then subtracted the "before" K (.729 J) by the "after" K (.491 J) to get .238 J.
But... it said "The ball bounces up to a lower height than that from which it was dropped. This implies that the kinetic energy after the collision was less than the kinetic energy before the collision." So I thought I had mixed up the two terms, and threw a negative sign in front of my answer, but that warranted a "Not quite. Check through your calculations; you may have made a rounding error or used the wrong number of significant figures."
*edit* - It really was the wrong number of significant figure-rounding when calculating... that one is going to eat me forever if I don't stop it:shy:
Attachments
Last edited: