How Does Plate Alignment Affect Capacitance in Variable Capacitors?

[pc2-brazil]

Homework Statement

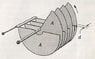
The figure (attached) shows a variable capacitor which uses air as the dielectric, of the kind used in the syntonization of radio devices. The plates are connected alternately; a group of them is fixed, while the other group can rotate around an axis. Consider a set of n plates of alternated polarity, each one of them having an area A and separated by the distance d. Show that the maximum value of the capacitance is:
C = \frac{(n-1)\epsilon_0 A}{d}

2. The attempt at a solution
It seems that there are (n - 1) plates in series, but this wouldn't lead to the expected result. According to the expected result, the capacitors would have to be in parallel, then, the maximum capacitance would occur when the movable plates aren't rotated with respect to the fixed plates. But it doesn't seem that they are in parallel. Could someone explain?

Thank you in advance.

 

[gneill]

Why do you think that the plates are in series? Can you draw a circuit diagram that corresponds to the scenario?

 

[pc2-brazil]

Why do you think that the plates are in series? Can you draw a circuit diagram that corresponds to the scenario?

The plates appear to be in series because each capacitor shares a plate with the adjacent one.

 

[gneill]

The plates appear to be in series because each capacitor shares a plate with the adjacent one.

But the plates are connected externally. There are two sets of plates that are interleaved. Each set is connected so that they share the same potential. Each plate "opposes" one or two plates of the opposite set. Each pair of 'opposing' plate surfaces represents a separate capacitor.