How Does Surface Tension Affect Bubble Separation in a Narrow Tube?

[zorro]

Homework Statement

An air bubble of radius R is formed on a narrow tube having a radius r where R>>r. Air of density ρ is blown inside the tube with velocity v. The air molecules collide perpendicularly with the wall of bubble and stop. Find the radius at which the bubble separates from the tube. Take the surface tension of bubble as T.

Homework Equations

The Attempt at a Solution

The bubble will will separate when the force exerted by the air molecules equals the force due to surface tension.
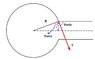
I am not sure of the direction of surface tension. For the bubble to cling to the tube, its direction might be as shown in the attachment.

Tsinθ terms get canceled as they act in opposite directions.
2Tcosθ x 2πr = ρ x πr² x v²
(I got RHS terms by finding the rate of change of momentum and hence the force )
I can't find out the value of coxθ

The answer is R=4T/ρv²

Any help appreciated.

 

[hikaru1221]

After coming this far, it all comes down to a simple geometry problem
Take a look at the picture: cos\theta = r/R

 

[zorro]

Thanks