- #1
Vibhor
- 971
- 40
Homework Statement
Homework Equations
The Attempt at a Solution
Pressure inside bubble = 2T/R
Buoyant force on bubble = ##\frac{4}{3} \pi R^3 ρ_w g ##
But I do not understand how surface tension is exerting force on the bubble .Also I do not understand the direction of surface tension force .
Please help me with the problem .
Thanks
Attachments
Last edited:
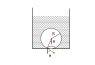
 . I am also feeling quite confused why this force should be pulling the bubble down instead of pulling it up ( i.e at 180 ° opposite to the green vector shown in image in post #7) ??
. I am also feeling quite confused why this force should be pulling the bubble down instead of pulling it up ( i.e at 180 ° opposite to the green vector shown in image in post #7) ??