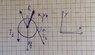fedecolo
- 61
- 1
Homework Statement
In the figure there are a block 1 of mass ##M##, a pulley (disk) of mass ##M## and radius ##R## and a second block of mass ##2M## on an inclined plane with an angle ##\alpha## with respect to the horizontal. On this plane the static friction is ##\mu##.
The wire does NOT slip on the pulley (so there is friction on the pulley too, but it says that the tension ##T_1 \not= T_2##).
What is the condition that ##\alpha## must satisfy such that the block 1 moves downward?
Homework Equations
The Attempt at a Solution
I wrote the diagram of forces for all the elements (with the systems of reference in the figure) and the torques with respect to the center of mass of the pulley.
For the block 1: ##T_1 - Mg= M(-a)##
For the pulley:
$$\begin{cases}
R_y -Mg -T_1 -T_2 \sin\alpha=0 \\ -R_x +T_2 \cos\alpha=0 \\
\end{cases}$$
##R## is the vincolar reaction of the pulley support.
For the block 2 (the system of reference is different!)
$$\begin{cases}
T_2-f_s -2Mg\sin\alpha =2Ma \\ 2Mg\cos\alpha -N=0
\end{cases}$$
Now using the fact that ##\sum \vec{M} = I_{CoM} \cdot \alpha_z## (##\alpha_z=\frac{a}{R}## is the angular acceleration of the pulley, sorry for the bad notation similar to the angle) I find the torques with respect to the center of mass of the pulley:
$$ \hat{u_z}: RT_1 -RT_2 \sin\alpha = 1/2 MR^2 \alpha_z$$
Now I can't solve this big system!
The condition is ##T_2 -2Mg\sin\alpha +2Ma \geq f_{s,MAX} = 2Mg\cos\alpha \cdot \mu##.
It seems that I must use the ##R## to find ##T_1## or ##T_2## but I have two different ##R_x## and ##R_y##...
Any help?