How Does the Distance y Change When Mass x Varies in a Pulley System?

[person123]

I was working on a pulley system as shown here:

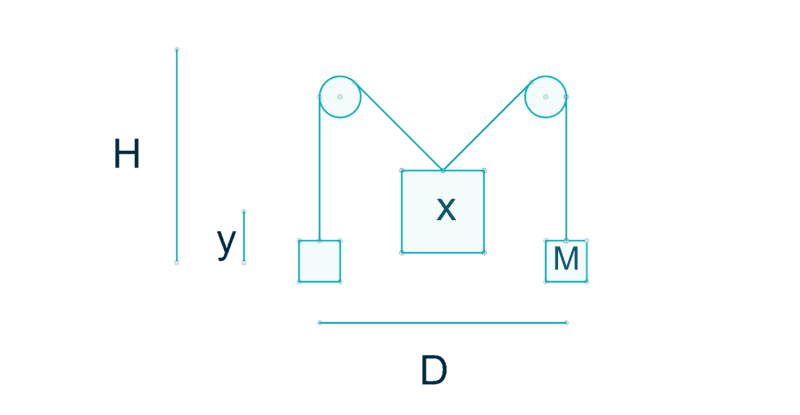
The mass on the right and left side is equivalent, and I am solving for when the system is in static equilibrium. Theta is the angle between the rope on either side of one of the pulleys. H and y are both measured from the original position of mass M, not its current location (it was simply meant as a reference point). The mass of the rope and friction are ignored. I wanted to find how the distance y changes as the mass x changes.

I first found the acceleration of the object, which is of course 0:

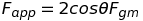
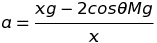
I then solved for theta, giving me:

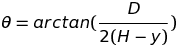
I then was able to find cosΘ:

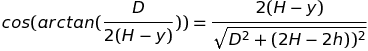
And I was then able to find the final equation by setting the first equation equal to 0:

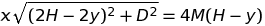
Here is a link to the graph: https://www.desmos.com/calculator/wpttkfsvmb

I imagine that this system may be used as a balance, in which the sag of the rope tells you the mass of x as based on the equation. Would that be possible? Thanks in advance.

(As a side note, I feel dumb showing my work in the form of images, but I can't figure out how to use BB code editor—I might just be missing something obvious).

 

[andrewkirk]

I imagine that this system may be used as a balance, in which the sag of the rope tells you the mass of x as based on the equation. Would that be possible?

Yes it can be used as a balance. It's the angle of the rope to the vertical, not the sag, that tells us the weight of the central mass.

 

[person123]

Yes it can be used as a balance. It's the angle of the rope to the vertical, not the sag, that tells us the weight of the central mass.

Could you also use the equation to find the mass of the object based on the vertical descent, or the change in y? (It may have been inaccurate to call that a sag).

 

[andrewkirk]

Could you also use the equation to find the mass of the object based on the vertical descent, or the change in y? (It may have been inaccurate to call that a sag).

No. We need the absolute level of y, not just its change, in order to calculate the angle. And we need the angle in order to calculate the force.

 

[person123]

No. We need the absolute level of y, not just its change, in order to calculate the angle. And we need the angle in order to calculate the force.

Yes—so if you were to know y, or the vertical position of the mass m, would you be able to determine the mass based on the formula I wrote? I should have wrote the value of y instead of the change in y.

 

[andrewkirk]

Yes—so if you were to know y, or the vertical position of the mass m, would you be able to determine the mass based on the formula I wrote? I should have wrote the value of y instead of the change in y.

Yes we could determine the mass based on a formula of that sort. I have not checked the calculations to see whether the formula is exactly correct.