- #1
Zack K
- 166
- 6
I understand Faraday's law and about induced electric fields created by a changing magnetic fields, etc.
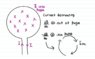
But what causes the current to oscillate in an LC circuit, with no battery? If you picture that there is current going into an inductor, and that current is decreasing over time, then you would see a curly electric field being produced in the direction of the current flow. (I uploaded an image for my reasoning)
Also, why would the current decrease at all? If inductors "oppose" change, wouldn't it make sense that the curly electric pushes the current to counteract the decreasing Coulombic electric fields?
But what causes the current to oscillate in an LC circuit, with no battery? If you picture that there is current going into an inductor, and that current is decreasing over time, then you would see a curly electric field being produced in the direction of the current flow. (I uploaded an image for my reasoning)
Also, why would the current decrease at all? If inductors "oppose" change, wouldn't it make sense that the curly electric pushes the current to counteract the decreasing Coulombic electric fields?