How Is Fluid Pressure Calculated in a U-Tube Experiment?

[Linus Pauling]

1.

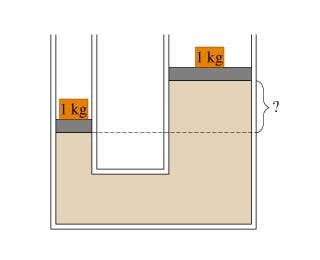
The locations of the two caps at equilibrium are now as given in this figure. (Part D figure) The dashed line represents the level of the water in the left arm.
What is the mass of the water located in the right arm between the dashed line and the right cap?



3. p - p_0 +rho*g*d

The pressure at the dashed line is 1kg / pi*r^2. I take r to be 1, so p = 1/pi
p_0, the pressure at the top of the right tube is 1kg / pi*(2r)^2 = 1/4pi

With these two values, and rho = density of water = 1000 kg/m^3, I solve for d and obtain:

d = 2.44*10^-5

I multiply that by A on the right tube to get volume = 4pi(2.44*10^-5) = 3.07*10^-4

Multiply by denisty to obtain mass, m = 0.307 which is incorrect.

 

[Delphi51]

The pressure due to the mass on the left at the dashed line is
P = F/A = mg/A = 1*g/A
so it pushes upward on the right side (at the dashed line) with force
F = PA = 1*g.
This upward force must equal the weight of the mass and extra liquid on the right. It results in an answer about 10 times as large as you have.