tigerseye
- 16
- 0
I'm stumped on this question:
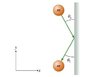
A ball of mass m moving with velocity v_i strikes a vertical wall. The angle between the ball's initial velocity vector and the wall is theta_i as shown on the diagram. The duration of the collision between the ball and the wall is delta t, and this collision is completely elastic. Friction is negligible, so the ball does not start spinning. In this collision, the force exerted on the ball by the wall is parallel to the x axis.
What is the magnitude F of the average force exerted on the ball by the wall?
I ended with F=(m*(v_ix))/(Deltat) but I think I messed up the algebra somehow.
A ball of mass m moving with velocity v_i strikes a vertical wall. The angle between the ball's initial velocity vector and the wall is theta_i as shown on the diagram. The duration of the collision between the ball and the wall is delta t, and this collision is completely elastic. Friction is negligible, so the ball does not start spinning. In this collision, the force exerted on the ball by the wall is parallel to the x axis.
What is the magnitude F of the average force exerted on the ball by the wall?
I ended with F=(m*(v_ix))/(Deltat) but I think I messed up the algebra somehow.