How Is the Period of a Pendulum Affected by Inertia and Center of Mass?

[stunner5000pt]

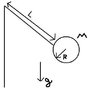
A heavy circular disc with radius R with mass M is fastened to a light string rod. The mass of the rod is negligible compared to the mass of the disc. The system can oscillate as a physical pendulum aout a fixed horizontal axis. The length of the rod is L.

Determine the period of small oscillations when the disc is fastened to the rod as shown, ie. when the disc swins in teh plane of the paper


force of gravity is $mg sin \theta$
the Inertia of the disc is $\frac{1}{4} MR^2$
the inertia due to the fact that the disc is fastened to the string L is
$$I = \frac{1}{4} MR^2 + M (R+L)^2$$
the force due to gracvity on the CM of the disc is Mg sin theta
not quite sure how to turn that into a torque, however...

 

[OlderDan]

The torque about the fixed point of rotation is due to the displacement of the disk from the center line. Express the distance betwen the center line in terms of L + R and multiply by the gravitational force.

OR

You already have the component of the gravitational force in the direction the disk can move. That component times the length L + R is the torque

 

[stunner5000pt]

so then the torque due to gravity is $Mg sin \theta (L+R)$??

and this sho7uld be equated to the torque due to the string?? Is that what should be done??

 

[OlderDan]

The "string" is actually a rigid rod with negligable mass. That is why this is a disk-rotation problem. The disk cannot move to the side without also rotating. The torque causes the angular velocity of the disk-rod system about the point of attachment to change.

Yes, the expression you have for the torque is correct. What does the torque do to the angular velocity? What is the equation that describes the relationship between the two?

 

[stunner5000pt]

the torque, $$\tau = I \alpha = I \omega R sin \theta$$
and $$I = \frac{1}{4} MR^2 + M(R^2 + L^2)$$
and the toqure due to gravity is $Mg(L+R) sin \theta$
am i on the right track??
but what do i do now?? the torque due to the gravity is not equal to the torque due to the string system...

 

[OlderDan]

$$\tau = I \alpha$$ is good. How do you know that $$\alpha = \omega R sin \theta$$

From $$\tau = I \alpha$$
I is a constant determined by the geometry of your system and the mass of the disk. You know that $$\alpha$$ is related to $$\theta$$ as the time rate of change of angular velocity, which is, in turn, the time rate of change of angular position $$\theta$$. The magic of this problem is in the phrase "small oscillations". If you recall the problem of an "ordinary" pendulum the same phrase was used. It permits the replacement of $$sin \theta$$ by the approximate equivalent $$\theta$$. You will then recognize that the torque is proportional to the negative of the angular displacement. This is directly analogous to the force being proportional to the negative of the linear displacement in linear simple harmonic motion problems. Your text probably has a general equation for the period of oscillation of a physical pendulum in terms of I, distance from the point of attacment to the center of mass, the mass and the acceleration of gravity. If not, see if you can come up with it by analogy to the problem of a mass on a spring where F = -kx

 

[stunner5000pt]

$$\alpha = \frac{g}{\frac{R^2}{4} + (R + L)^2}$$
so then $$T = 2 \pi \sqrt{{\frac{\frac{R^2}{4} + (R + L)^2}{g(L+R)}}$$
is this correct?

 

[maverick280857]

How can you say that $\alpha = \omega R \sin\theta$? (This is of course if you are referring to omega as the angular speed).

A better idea is to take the torque about the center of mass of the system and take the moment of inertia referred to that axis as well (first). This is really a physical pendulum and in your simple case, the system mass center coincides with that of the disk as the rod is assumed to be massless.

When you have the equation of motion, it should include a $\sin\theta$ term depending on what this angle is (its from the vertical right?). For small angle approximations, the motion is simple harmonic and you can extract the parameters of the motion from the equation, which should look like $I\ddot{\theta} + k\theta = 0$.

Cheers
Vivek

 

[dextercioby]

How did u get that $4$ in the moment of inertia ...?Doesn't the disk spin around an axis passing through its center of mass...?If so,then is should be $I=\frac{1}{2}MR^{2}$.

Daniel.

 

[OlderDan]

The disk is NOT spinning around its center.

Your result is {ALMOST} correct stunner500pt. The general result is

$$T = 2 \pi \sqrt{{\frac{I_{support}}{mgL_{cm}}}$$

You have {} identified the moment of inertia and the distance to the center of mass (L + R) in this problem.

Correction:

If the disk were rotating about its perpendicular axis the moment of inertia would be

$I= \frac{1}{2}MR^{2}$

So the first factor should be 1/2 not 1/4. Then because it is rotating about a point L + R from the center the moment of ineria becomes

$$I = \frac{1}{2} MR^2 + M (R+L)^2$$

The factor 1/4 would be appropriate for a disk spinning about an axis along a diameter through the center, which is not the case here.

I'm sure that was the point intended by dextercioby calling attention to the 4.

 

[maverick280857]

The disk is NOT spinning around its center.

Your result is correct stunner500pt. The general result is

$$T = 2 \pi \sqrt{{\frac{I_{support}}{mgL_{cm}}}$$

You have correctly identified the moment of inertia and the distance to the center of mass (L + R) in this problem.

Yes that's correct. The disk wouldn't be a pendulum if it were spinning about its CM dextercioby.