How Is Work Calculated on a Block Sliding Down a Frictionless Incline?

[maniacp08]

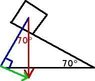
A 8 kg block slides down a frictionless incline making an angle of 70° with the horizontal.

(a) What is the total work done on the block when the block slides 2 m (measured along the incline)?
(b) What is the speed of the block after it has slid 1.5 m if it starts from rest?
m/s
(c) What is its speed after 1.5 m if it starts with an initial speed of 2 m

relevant equations:
Work = Force * Cos Theta * Displacement
Total Work = change in Kinetic Energy

There are two forces acting on the block, the normal force and force of gravity.
The normal force will do no work because it is perpendicular to the displacement.
So the net force will be the force of gravity?

Which is:
(8kg)(9.81m/s^2) * Cos (-160) * 2m = -147.5J

Please correct me if I am wrong anywhere. Thanks.

 

[Perillux]

You don't need the normal force because it is frictionless.
so to find the force (caused by gravity) perpendicular to the surface of the ramp, you would take the sine of 70 Not the cosine of -160.. So the same equation you have but change the Cos(-160) part to sin(70)

then you should be able to find the acceleration because we know the force of gravity pushing it down, and you can go from there to find the other answers.

 

[Perillux]

Look at my attached image to help you see why it is Sin(70).

The red arrow is the force of gravity. So we set up a right triangle with one of the components parallel to the surface of the ramp (green). and the blue component would be equivalent to the normal force (but it doesn't apply in this problem). Using some geometric properties you should be able to see that the red angle is also 70 degrees.
So the green component is
sin(70) * (force of gravity)

and that is the force pushing it down the ramp.

 

[maniacp08]

Is Cos because the work equation is

Work = Force * Cos Theta * Displacement

The Cos Theta is suppose to be the angle between the Force and Displacement.
Shouldn't it be Cos(70 + 20)?

I thought we shouldn't calculate Force components when calculating the Work.

 

[Doc Al]

relevant equations:
Work = Force * Cos Theta * Displacement
Total Work = change in Kinetic Energy

Good.

There are two forces acting on the block, the normal force and force of gravity.
The normal force will do no work because it is perpendicular to the displacement.

Good.

So the net force will be the force of gravity?

Which is:
(8kg)(9.81m/s^2) * Cos (-160) * 2m = -147.5J

Your mistake was taking the angle between gravity (down) and displacement up the incline. But the block slides down the incline. So the sign of your answer is wrong. The angle should be 20, not 160. Then the sign would be positive, as it should be.

 

[maniacp08]

Ahh, so I do not need to add the 70.
I only need to add it if is up the incline then.

Thanks for your help.

 

[maniacp08]

To Calculate answers for part B and C
I would just use the equation
Total work = change in kinetic energy correct?

 

[Doc Al]

That's right. (You'll have to recalculate the total work, since the displacement is different.)

 

[Doc Al]

I thought we shouldn't calculate Force components when calculating the Work.

Just an FYI: It's perfectly OK to break a force into components and find the work done by each component. In fact, that's often the easy way to solve the problem.

While there's nothing wrong with what you did (except what I already pointed out), the way I'd personally solve it is by breaking the weight into components parallel and perpendicular to the incline. Since I know that the perpendicular component does no work, we can just deal with the parallel component, which is mg sin(70) acting down the incline. Since that force and the displacement are in the same direction, cos(theta) = cos(0) = 1, and thus the work done equals just mg sin(70) d. (This is what Perillux was explaining.)

Note that sin(70) = cos(20), so the two methods give the same answer. (They better! )