Curieuse
- 51
- 1
1. Problem statement
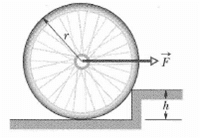
In figure, what magnitude of (constant) force F applied horizontally at the axle of the wheel is necessary to raise the wheel over an obstacle of height h=3.00cm ? The wheel's radius is r=6.00cm , and it's mass is m=0.800 kg.
Balance of forces: Fnet=0 (xy plane)
Balance of torques: τnet=0 (z axis)
3. The Attempt at a Solution
By balance of torques about point of contact with obstacle,
F(r-h)=mgr
I chose that point so as to not account for forces of contact there!
The answer i got
F=(mgr)/(r-h)
F= 15.7 N
The answer at the back of the text is 13.6N.
What did i do wrong?
Also i have this lingering doubt, will the normal forces at the point of contact with the horizontal floor , be included?
I worked another problem where the solution i found ignored it and when i tried putting it in, it simply nullifies the weight , which lead to unreasonable answers... But still why is it not to be included? I mean it's also a force no.. Of course it disappears as soon as the wheel lifts off due to that horizontal F .. Thanks in advance..
 [/B]
[/B]
In figure, what magnitude of (constant) force F applied horizontally at the axle of the wheel is necessary to raise the wheel over an obstacle of height h=3.00cm ? The wheel's radius is r=6.00cm , and it's mass is m=0.800 kg.
Homework Equations
Balance of forces: Fnet=0 (xy plane)
Balance of torques: τnet=0 (z axis)
3. The Attempt at a Solution
By balance of torques about point of contact with obstacle,
F(r-h)=mgr
I chose that point so as to not account for forces of contact there!
The answer i got
F=(mgr)/(r-h)
F= 15.7 N
The answer at the back of the text is 13.6N.

What did i do wrong?
Also i have this lingering doubt, will the normal forces at the point of contact with the horizontal floor , be included?
I worked another problem where the solution i found ignored it and when i tried putting it in, it simply nullifies the weight , which lead to unreasonable answers... But still why is it not to be included? I mean it's also a force no.. Of course it disappears as soon as the wheel lifts off due to that horizontal F .. Thanks in advance..