SUMMARY
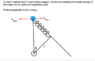
The discussion focuses on calculating the total kinetic energy of a system in circular motion using the Lagrangian mechanics approach, specifically the equation L = T - V. Participants highlight the importance of correctly defining variables such as tangential velocity (vtan) and angular velocity (ω) to avoid dimensional inconsistencies. A key takeaway is the necessity of accurately accounting for the signs of radial and angular components when deriving equations. The final expression for kinetic energy should reflect the correct relationships between these variables.
PREREQUISITES
- Understanding of Lagrangian mechanics and the equation L = T - V
- Familiarity with circular motion concepts, including tangential velocity and angular velocity
- Ability to differentiate functions with respect to time to find velocity
- Knowledge of vector representation in physics
NEXT STEPS
- Study the derivation of kinetic energy in Lagrangian mechanics
- Learn about the relationship between radial and tangential components in circular motion
- Explore the implications of dimensional analysis in physics equations
- Investigate vector calculus applications in motion analysis
USEFUL FOR
Students and educators in physics, particularly those studying mechanics, as well as anyone interested in applying Lagrangian methods to analyze motion in circular systems.