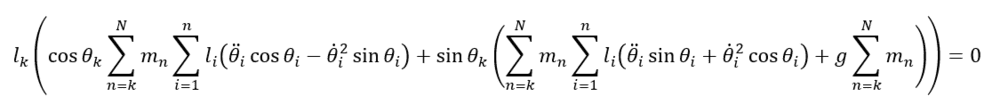How to calculate acceleration of blobs in any degree pendulum?

[Rafums]

I want to create a method to calculate acceleration of blobs in any degree pendulum (double, triple and more). I have this equation but I am not sure if it is correct, or how to extract acceleration from it.

[Mentor Note -- this is a new thread start to correct errors in the previous 2 thread starts]

 

[anuttarasammyak]

In the configuration as attached sketch for 2D n-fold pendulum shows
(x_0,y_0)=(0,0)
(x_i,y_i)=(x_{i-1},y_{1-1})+(l_i \cos\theta_i, l_i \sin\theta_i)=(\sum_{j=1}^i l_j\cos\theta_j, \sum_{j=1}^i l_j\sin\theta_j)
(\dot{x_i},\dot{y_i})=(\sum_{j=1}^i l_j (-\sin\theta_j) \dot{\theta_j}, \sum_{j=1}^i l_j\cos\theta_j \dot{\theta_j})

Lagrangean of the system is
L=\sum_{i=1}^n \frac{m_i}{2}(\dot{x_i}^2+\dot{y_i}^2)+g\sum_{i=1}^n m_i x_i
with gravity force applying to x positive direction. Express L as $L(\theta_1, \theta_2,...,\theta_n, \dot{\theta_1}, \dot{\theta_2}, ... , \dot{\theta_n})$

L=\sum_{i=1}^n \frac{m_i}{2}[\{\sum_{j=1}^i l_j (-\sin\theta_j) \dot{\theta_j}\}^2+\{\sum_{j=1}^i l_j \cos\theta_j\ \dot{\theta_j}\}^2]+g\sum_{i=1}^n m_i \sum_{j=1}^i l_j\cos\theta_j

We get equation of motion or Lagrangean equation from this Lagrangean, e.g.

\frac{d}{dt}\frac{\partial L}{\partial \dot{\theta_k}}=\frac{d}{dt}\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k \cos\theta_k]
=\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\cos\theta_j) \dot{\theta_j}^2\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j (-\sin\theta_j\ \dot{\theta_j}^2\}l_k \cos\theta_k]
+\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \ddot{\theta_j}\}l_k (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \ddot{\theta_j}\}l_k \cos\theta_k]
+\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\cos\theta_k)\dot{\theta_k}+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k(- \sin\theta_k) \dot{\theta_k}]
equals to
\frac{\partial L}{\partial \theta_k}=\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\sin\theta_j) \dot{\theta_j}\}l_k (-\cos\theta_k)\dot{\theta_k}+\{\sum_{j=k}^i l_j \cos\theta_j\ \dot{\theta_j}\}l_k (-\sin\theta_k)\dot{\theta_k}]+g\sum_{i=k}^n m_i \ l_k(-\sin\theta_k)

So the resulted equation is
\sum_{i=k}^n m_i[\{\sum_{j=k}^i l_j (-\cos\theta_j) \dot{\theta_j}^2\} (-\sin\theta_k)+\{\sum_{j=k}^i l_j (-\sin\theta_j)\ \dot{\theta_j}^2\} \cos\theta_k<br /> +\{\sum_{j=k}^i l_j (-\sin\theta_j) \ddot{\theta_j}\} (-\sin\theta_k)+\{\sum_{j=k}^i l_j \cos\theta_j\ \ddot{\theta_j}\}\cos\theta_k<br /> -g (-\sin\theta_k) ]=0
or
\sum_{i=k}^n m_i[\ \sum_{j=k}^i l_j \sin(\theta_k-\theta_j) \dot{\theta_j}^2<br /> +\sum_{j=k}^i l_j \cos(\theta_k-\theta_j )\ddot{\theta_j} +g \sin\theta_k\ \ ]=0

where k=1,2,...,n. Coefficients of g have trigonometric function though formula OP does not have it.　　

These n equations give you formula of $\ddot{\theta_k}$ as functions of $\theta_i$s and $\dot{\theta_i}$s, which you are looking for.

 

[Rafums]

I found this equation:

It comes from this page: https://www.researchgate.net/publication/336868500_Equations_of_Motion_Formulation_of_a_Pendulum_Containing_N-point_Masses and I transformed them like this:

Did I do it right?

 

[anuttarasammyak]

How about checking it for n=1, a simple pendulum.
You should get
l_1 \ddot{\theta_1}+g \sin\theta_1=0.

If it's OK proceed to check it for n=2. You should get $\ddot{\theta_1},\ddot{\theta_2}$ as function of $\theta_1,\theta_2,\dot{\theta_1},\dot{\theta_2}$ which is calculated from (19) and (20) of the paper you quote.