D44
- 70
- 0
Hi guys
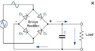
I'm working on a few questions regarding the full wave rectifier circuit similar to the attached image.
The AC voltage is 12v at 110Hz, the ripple voltage is 1v peak to peak and the load current is 24mA. I am to assume each diode has a forward voltage drop of 1v when conducting.
I have to find:
1) The length of time the capacitor is supplying current to the load for if the diode conduction angle is 20 degrees.
2) Value of capacitor required to produce the 1v peak to peak ripple voltage.
3) Average power dissipated in the load.
For question 1, I found the period = 1/(2*110) = 1/220 = 4.55ms, then dt = 4.55-(4.55/6) = 3.79ms. Where (4.55/6) was the period of the capacitor charging.
For question 2, I then used I=c(dv/dt) and transposed for c = I(dt/dv). Therefore c = 24x10-3*(3.79x10-3/1) = 90.96 micro Farads.
For question 3, I used P = I*(Vac - Vdrop) = 24x10-3*(12-2) = 0.24W. This doesn't seem right to me.
I'd appreciate your help as I'm not confident that any of them are correct.
Thanks
I'm working on a few questions regarding the full wave rectifier circuit similar to the attached image.
The AC voltage is 12v at 110Hz, the ripple voltage is 1v peak to peak and the load current is 24mA. I am to assume each diode has a forward voltage drop of 1v when conducting.
I have to find:
1) The length of time the capacitor is supplying current to the load for if the diode conduction angle is 20 degrees.
2) Value of capacitor required to produce the 1v peak to peak ripple voltage.
3) Average power dissipated in the load.
For question 1, I found the period = 1/(2*110) = 1/220 = 4.55ms, then dt = 4.55-(4.55/6) = 3.79ms. Where (4.55/6) was the period of the capacitor charging.
For question 2, I then used I=c(dv/dt) and transposed for c = I(dt/dv). Therefore c = 24x10-3*(3.79x10-3/1) = 90.96 micro Farads.
For question 3, I used P = I*(Vac - Vdrop) = 24x10-3*(12-2) = 0.24W. This doesn't seem right to me.
I'd appreciate your help as I'm not confident that any of them are correct.
Thanks