How to Calculate Surface Integral Using Stokes' Theorem?

[WMDhamnekar]

TL;DR

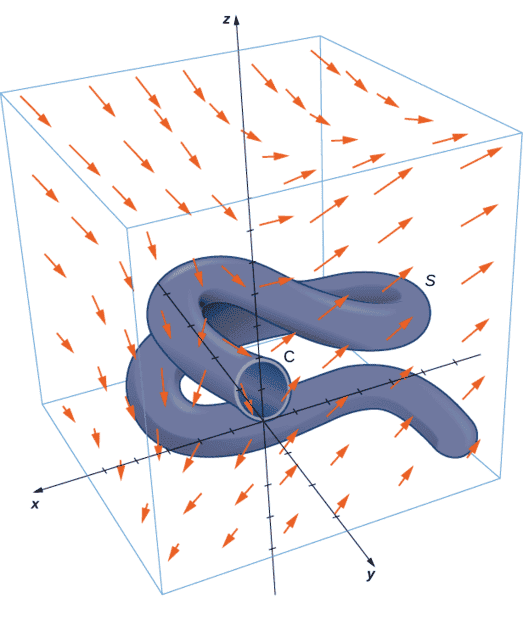
Stokes’ theorem translates between the flux integral of surface S $\displaystyle\iint\limits_{\Sigma} f \cdot d\sigma$ to $\displaystyle\int\limits_C f\cdot dr$ a line integral around the boundary of S. Therefore, the theorem allows us to compute surface integrals or line integrals that would ordinarily be quite difficult by translating the line integral into a surface integral or vice versa.
Calculating a surface integral

Calculate surface integral $\displaystyle\iint\limits_S curl F \cdot dS$ where S is the surface, oriented outward in below given figure and F = [ z,2xy,x+y].

How can we answer this question?

 

[pasmith]

You would do that as a line integral over $C$; I assume the question tells you what $C$ is?