Dency Dela Cruz
- 2
- 0
Hi,
I am doing design calculations for a Variable Pitch Propeller and I have to calculate bearing life. A deep groove ball bearing is used for a mainshaft (driveshaft). And the mainshaft is connected to the propeller hub.
I know the basic formula for calculating the bearing life but I am having trouble in regards with determining the equivalent dynamic load needed for the calculation. This equivalent dynamic load can be calculated by knowing the applied axial load on the bearing (due to thrust) and an applied radial loading.
I am able to calculate the axial loading due to thrust but not sure on how to go about determing the radial load on the bearing nor what is the factor the causes this load. Can anyone help me on how to go about this?
Below is an illustration of the arrangement.
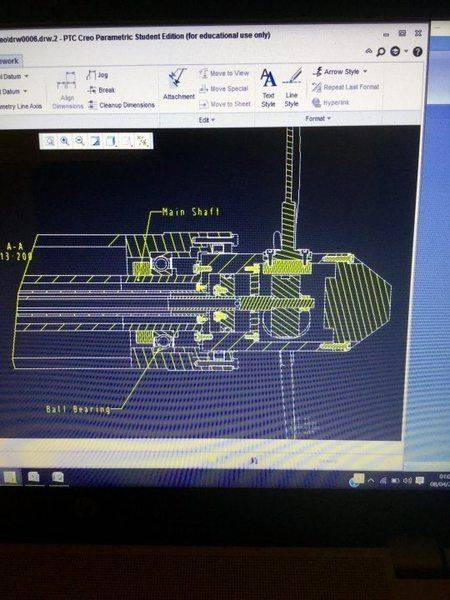
Thank you
I am doing design calculations for a Variable Pitch Propeller and I have to calculate bearing life. A deep groove ball bearing is used for a mainshaft (driveshaft). And the mainshaft is connected to the propeller hub.
I know the basic formula for calculating the bearing life but I am having trouble in regards with determining the equivalent dynamic load needed for the calculation. This equivalent dynamic load can be calculated by knowing the applied axial load on the bearing (due to thrust) and an applied radial loading.
I am able to calculate the axial loading due to thrust but not sure on how to go about determing the radial load on the bearing nor what is the factor the causes this load. Can anyone help me on how to go about this?
Below is an illustration of the arrangement.
Thank you