How to calculate the Electric Field due to Capacitors?

[Jason E]

I have a problem that I have encountered during research.

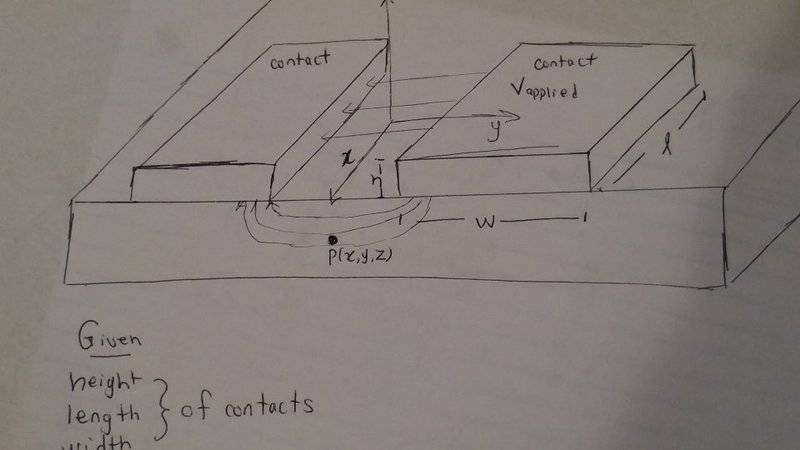
The setup for this scenario is that I am placing two contacts on top of a piece of diamond. What I need to be able to do is calculate the Electric Field at a point within the diamond when I apply a voltage to the contact. The point of interest is in between the two contacts but below them (as shown in the crude image I have made.)

Some of the things I am confused about

1. How are the charges accumulated on these contacts? In order for there to be an Electric Field at point P the charges can't only accumulate on the inside of the plate.

2. How would I calculate the total charge on the capacitor?

In order to simplify the problem I assume that we are finding the value of the Electric Field for a P close to the center of the contacts, meaning that the x-axis will not play a role in my calculation. So I need to be able to calculate the Electric Field contribution due to a cross sectional area, like shown below

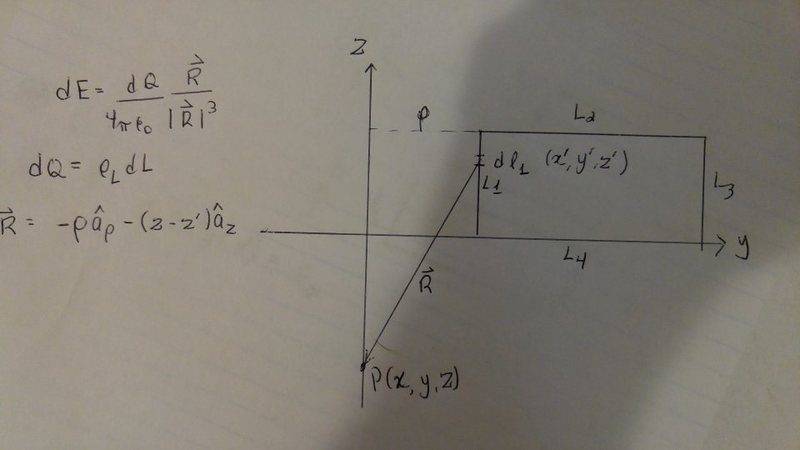
However if I am taking a cross sectional area, the middle of this cross section can't have an accumulated charge only the edges can. I reasoned this because if we were to translate it back to the total volume, having a charge across the cross section would mean that the charges were spread out through the volume meanwhile the charges should be accumulating on the surface only.

Assuming this is correct I need to find a line charge density ρL. In order to do this I need to know what the total charge would be. I am unsure of using the general parallel plate capacitor formula Q = CV.

Secondly I am not sure how the sides will actually contribute to the Electric field at point P. It seems as though only the bottom of the plate will contribute to the Electric Field at that point.

One of the researchers I asked said that we can assume each side of the contact accumulates the same charge in order to simplify the problem but I am still unsure of the whole setup.

If you can help I'd appreciate it very much. I can also show any mathematical related work I have done

 

[berkeman]

Welcome to the PF.

Do you have access to simulation software like Ansys or COMSOL?

 

[Jason E]

Welcome to the PF.

Do you have access to simulation software like Ansys or COMSOL?

No I do not. I'm basically supposed to write code to simulate what the field will be

 

[f95toli]

You might be able to find an (approximate) calculation of the E-field in a book on RF/microwave transmission lines. The geometry in your sketch is basically that of a coplanar stripline.
If you do this analytically you will end up with a bunch of elliptical integrals.

 

[Jason E]

You might be able to find an (approximate) calculation of the E-field in a book on RF/microwave transmission lines. The geometry in your sketch is basically that of a coplanar stripline.
If you do this analytically you will end up with a bunch of elliptical integrals.

I should have mentioned this is a DC voltage, there are no waves involved.

So the coplanar stripline produces an electric field in what way that is different than a regular parallel plate capacitor?

Is there any way to just simplify this problem? I want at least a general understanding of how the charges are accumulated on the contact with a DC voltage.

My work with transmission lines has only been with respect to wave propagation, my textbook doesn't really cover exactly what I'm trying to understand here.

Could I just assume the outside surface of the contacts accumulate equal charge in order to simplify the problem?

Sorry for the loads of questions, there's just a lot of confusion.

 

[f95toli]

I realized that you were talking about the DC case. However, when dealing with transmission lines we are usually interested in calculating the impedance per unit length and the usual way of doing that is to simply calculate the capacitance between the conductors in the electrostatic (DC) case (this works because the typical dimensions in the XY plane are much smaller than the wavelength).
Hence, my idea (which might not work) was simply that since your geometry looks a bit like a (short) piece of coplanar stripline you might be able to use some of the same methods/results.

Have a look in e.g. Simons book on coplanar waveguide circuits.

Note that you won't be able to calculate this analytically without some serious approximations. In the general case you will inevitably need a FEM solver of some sort.

 

[Baluncore]

The gradient of the electric field on the midpoint line could be quickly estimated, probably to +/–25%.
How accurately do you need to know it ?

The scenario you have defined is asymmetric and so has no trivial solution. Having air rather than a conductor under the slab makes it difficult because the boundary condition is not constrained. Is it possible to select a different model that could be symmetric such as by having a ground plane or by duplicating the top conductors below the slab ?

All the charges in a capacitor move one way a bit. That includes the volume of the diamond slab. You need to stop thinking about movement and accumulation of charge as it will only confuse the capacitance and field calculation.

The dielectric constant of diamond will change the field pattern where it contacts the surrounding space. Do you know what the low frequency ε_r is for your diamond?

 

[Jason E]

The gradient of the electric field on the midpoint line could be quickly estimated, probably to +/–25%.
How accurately do you need to know it ?

The scenario you have defined is asymmetric and so has no trivial solution. Having air rather than a conductor under the slab makes it difficult because the boundary condition is not constrained. Is it possible to select a different model that could be symmetric such as by having a ground plane or by duplicating the top conductors below the slab ?

All the charges in a capacitor move one way a bit. That includes the volume of the diamond slab. You need to stop thinking about movement and accumulation of charge as it will only confuse the capacitance and field calculation.

The dielectric constant of diamond will change the field pattern where it contacts the surrounding space. Do you know what the low frequency ε_r is for your diamond?

I don't need to know it precisely, I'd say within 25% estimation would be just fine. However I am starting with the midpoint to simplify. I need a general formula to be able to calculate the field at multiple points not just the midpoint (even if the midpoint might prove most useful)

Also we're assuming the diamond slab is large enough to neglect the air boundary below the diamond slab. Even so I can model it to be placed atop a conductor, it doesn't have to be air.

Isn't the placement of the charges important in qualitatively assessing the problem?

And how do I calculate the Capacitance? I feel as though it's not a simple parallel plate capacitor in this scenario.

I don't know the relative permittivity of the diamond right now, I was planning on just leaving it as a variable until the end.

My basic gripe is just how I need set up this problem. Analytically it seems to me the bottom part of the contact has the most significant Electric Field contribution at point P but then how would I calculate capacitance and the such?