How to calculate the gear ratio of this compound planetary gearset?

[PlanetaryGearbox]

Yellow is sun, dark blue and red are planets , green is idler.
Teeth of sun: 30 and 100
Teeth of blue planet: 30 and 70
Teeth of red planet: 30
Teeth of ring: 200
Teeth of idler: 55

The aim is to achieve the same degree of rotation (but in opposite directions)) of carrier carrying blue planet as of the carrier carrying the red planet.

I am able to achieve the above with trial and error on CAD, but cannot understand the calculations on paper.

Is there a book or website I can refer too?

 

[Lnewqban]

Welcome, PG!

This may help:
https://www.tec-science.com/mechani...-equation-of-planetary-gears-willis-equation/

 

[PlanetaryGearbox]

Thanks! I have been following the same page for my calculations but the problem is that they assume that the same planet gear meshes with the ring and sun, but in my case those two gears are different (albeit compounded).

Update: I found a paper which contained the formula for compounded gears in planetary gear train, and it matches what I see in CAD!

But I am still not able to calculate the movement of the red gear with the green idler. The formulae on wikipedia for idler gear are the same as regular system.

 

[Juanda]

Thanks! I have been following the same page for my calculations but the problem is that they assume that the same planet gear meshes with the ring and sun, but in my case those two gears are different (albeit compounded).

Update: I found a paper which contained the formula for compounded gears in planetary gear train, and it matches what I see in CAD!

But I am still not able to calculate the movement of the red gear with the green idler. The formulae on wikipedia for idler gear are the same as regular system.

Could you share the paper?

Since you're still having some trouble I gave it a shot using the same method as the one in the link from a previous answer by @Lnewqban.

I'm not sure of the procedure and I might be reinventing the wheel here (most likely with errors which is why I'd like to read that paper you mentioned) but you could try inputting the values in your CAD model to check it.

There are 6 bodies. From top to bottom, they are:

1. Cyan gear $\theta_c$, $d_c$
2. Blue gear $\theta_b$, $d_b$
3. Yellow gear $\theta_y$
   • Big diameter $d_{yb}$
   • Small diameter $d_{ys}$
4. Transparent carrier $\theta_t$, $d_t$
5. Green gear $\theta_g$, $d_g$
6. Red gear $\theta_r$, $d_r$

I used the superposition of each possible motion on different bodies caused by its immediate neighbors like in the previous link.

Starting with the green gear which is similar to the planet from the link.

• If the transparent carrier moved while the gears slide: $\theta_g = \theta_t$
• If the green gear rotated around the yellow gear: $\theta_g = \frac{d_{ys}}{d_g}\theta_t$
• If the green and yellow gears rotated while their centers don't move: $\theta_g = -\frac{d_{ys}}{d_g}\theta_y$
• If the red and green gears rotated while their centers don't move: $\theta_g= -\frac{d_r}{d_g}\theta_r$
• If the green gear rotated around the red gear: This is analogous to the second point. However, it seems impossible because of the carrier so I don't think this equation should be added. Besides, I'm not sure I can't come up with that equation myself now. Additionally, as later seen in the analysis for the blue gear, I now think that, if there is no carrier joining the two gears in a way to enforce that motion, this equation should not be considered.

Finally, using superposition for all the movements:
$$\theta_g = \theta_t + \frac{d_{ys}}{d_g}\theta_t - \frac{d_{ys}}{d_g}\theta_y - \frac{d_r}{d_g}\theta_r$$

Then, applying the same methodology to the red gear:

• If the transparent carrier moved while the gears slide: $\theta_r = \theta_t$
• If the green and red gears rotated while their centers don't move: $\theta_r = -\frac{d_{g}}{d_r}\theta_g$
• If the red gear rotated around the green gear: Again, not possible due to the transparent carrier. Similar to the last point studied in the green gear.
• If the cyan and red gears rotated while their centers don't move: $\theta_r = \frac{d_{c}}{d_r}\theta_c$
• If the red gear rotated around the cyan gear: $\theta_r = \frac{d_{c}}{d_r}\theta_t$

The combined movement of the red gear would be:
$$\theta_r = \theta_t - \frac{d_{g}}{d_r}\theta_g + \frac{d_{c}}{d_r}\theta_c + \frac{d_{c}}{d_r}\theta_t$$

Lastly, for the blue gear:

• If the blue and yellow gears rotated while their centers don't move: $\theta_b = -\frac{d_{yb}}{d_b}\theta_y$
• If the cyan and blue gears rotated while their centers don't move: $\theta_b = \frac{d_{c}}{d_b}\theta_c$
• If the blue gear rotated around the yellow gear: This equation has been involving the transparent carrier so far but there is no carrier in this couple. I guess we don't write the equation because there is nothing to force this movement. The movement might just emerge from the other equations as shown in your pictures.
• If the blue gear rotated around the cyan gear: This equation has been involving the transparent carrier so far but there is no carrier in this couple. I guess we don't write the equation because there is nothing to force this movement. The movement might just emerge from the other equations as shown in your pictures.

Therefore, the resultant movement will be:
$$\theta_b = -\frac{d_{yb}}{d_b}\theta_y + \frac{d_{c}}{d_b}\theta_c$$

I feel with those 3 equations all the bodies should be defined. As shown in the link, you can write them in terms of angular speeds and diameters or number of teeth as preferred.

 

[Juanda]

I'm not sure of the procedure and I might be reinventing the wheel here (most likely with errors which is why I'd like to read that paper you mentioned) but you could try inputting the values in your CAD model to check it.

What I suspected is beginning to be a certainty. There must be something wrong with the method I tried.
I tested with a simpler system and I got non-sensical results.

From the previous derivation, for a system like shown the equations should be:
$$\theta_g = \theta_t + \frac{d_{ys}}{d_g}\theta_t - \frac{d_{ys}}{d_g}\theta_y - \frac{d_r}{d_g}\theta_r$$
$$\theta_r = \theta_t - \frac{d_{g}}{d_r}\theta_g$$

Substituting the second equation into the first one:
$$\theta_g = \theta_t + \frac{d_{ys}}{d_g}\theta_t - \frac{d_{ys}}{d_g}\theta_y - \frac{d_r}{d_g}(\theta_t - \frac{d_{g}}{d_r}\theta_g)$$

Symplyfying, $\theta_g$ disappears. Which could be OK. It could mean that the angle is defined by the other parameters. However, the result I get makes no sense.
$$\theta_y = \frac{d_g}{d_{ys}}(1+\frac{d_{ys}}{d_g}- \frac{d_r}{d_g})\theta_t$$
The problem with that result is that, in reality, I could stop the rotation of the transparent carrier and turn the sun. That should be a valid solution. However, according to that equation, if I stop the carrier the sun should be stopped too.
In conclusion, my derivation is not correct and I don't know how to do it correctly.

The way to obtain the correct solution for a system like that would be to consider the green gear as the sun and the other two as its planets using the information from the link as reference but knowing that the angular displacement of the carrier is the same for both planets. Maybe by solving it that way, I'll be able to extrapolate some useful conclusion but it'll have to wait for tomorrow because I can't continue now.

 

[PlanetaryGearbox]

Thank you @Juanda for such a detailed reply.

In the end I could only figure out the calculations for the compounded gear (from the paper), but not for the one with idler gear. If I use two idler gears, and keep the size of the planet, sun, and ring the same then I get the exact results in CAD as from the formulae for system with idler on wikipedia. So, the formulae on wikipedia for idler system are definitely wrong, but I didn't have high hopes from wikipedia anyway.

I trusted the CAD in the end and froze the system. I am sending it for prorotyping and see what happens. Today, I will check out your calculations too and try them with my system and get back to you soon. Thanks again!!!

Here is the link to the paper (a friend of mine had access to it) where I got the calculations for planetary system with compound gears:
https://link.springer.com/article/10.1007/s10010-023-00702-6

 

[Juanda]

View attachment 350274
The way to obtain the correct solution for a system like that would be to consider the green gear as the sun and the other two as its planets using the information from the link as reference but knowing that the angular displacement of the carrier is the same for both planets. Maybe by solving it that way, I'll be able to extrapolate some useful conclusion but it'll have to wait for tomorrow because I can't continue now.

I'll try to obtain the expression for the yellow gear again.

Considering the green gear is the sun and the yellow gear is its planet connected by the transparent carrier.
$$\theta_y = \theta_t + \frac{d_{g}}{d_y}\theta_t - \frac{d_{g}}{d_y}\theta_g \tag{1}$$
Considering the green gear is the sun and the red gear is its planet connected by the transparent carrier.
$$\theta_r = \theta_t + \frac{d_{g}}{d_r}\theta_t - \frac{d_{g}}{d_r}\theta_g \tag{2}$$
Knowing the carrier is the same in both equations, I'll obtain the carrier's angle from the second equation to plug it into the first one.
$$\theta_t = \frac{\theta_r+\frac{d_g}{d_r}\theta_g}{1+\frac{d_g}{d_r}} = \frac{d_r\theta_r+d_g\theta_g}{d_r+d_g} \tag{3}$$
Plugging that into the first equation:
$$\theta_y = (\frac{d_r\theta_r+d_g\theta_g}{d_r+d_g}) + \frac{d_{g}}{d_y}(\frac{d_r\theta_r+d_g\theta_g}{d_r+d_g}) - \frac{d_{g}}{d_y}\theta_g \tag{4}$$
The equation $(4)$, no matter what we try, is VERY different from what I obtained in the previous post.

$$\theta_y = \frac{d_g}{d_{y}}(1+\frac{d_{y}}{d_g}- \frac{d_r}{d_g})\theta_t$$

To sum up, I think what's derived in this post is correct because I followed the same procedure as the link. But I don't know how to derive the formulas, even for this simplified system, if there are any changes introduced...
I realized you just shared the paper as I was writing this reply. I'll read it and maybe I can understand the mechanical links and their governing equations better.

 

[Juanda]

Here is the link to the paper (a friend of mine had access to it) where I got the calculations for planetary system with compound gears:
https://link.springer.com/article/10.1007/s10010-023-00702-6

I'll keep looking for sources on this.
So far I found this but I believe it's not the same mechanism.
Master thesis: Design of a Compound Planetary Gearset

It seems like these gears are not engaging anything though...

I need to read more about it.

 

[PlanetaryGearbox]

https://we.tl/t-57fpOcfZHr

Here's a link to the paper that I had referred to. @Juanda

It is a different paper from the one you have shared. But it doesn't show the changes in velocity or angles, just the final formula.

 

[Juanda]

https://we.tl/t-57fpOcfZHr

Here's a link to the paper that I had referred to. @Juanda

It is a different paper from the one you have shared. But it doesn't show the changes in velocity or angles, just the final formula.

Before I start with the article, I'd like to keep going with the simplified system. I hope that by understanding the simple version we'll be able to extrapolate it easily to other systems.

View attachment 350274

I was able to obtain the same results as in the link for the yellow and green gears following a slightly different method which I believe should be applicable to other meshed gears. Then, I was also able to extrapolate it to the simplified system I presented with the red gear added to it and I got the same result as before when I considered the green gear to be the sun and followed the procedure from the link.

I did it by imposing the no-slipping condition and defining the velocity of the two meshed points from the different gears around the stationary axis located at the center of the sun (yellow) which is the reference frame for my formulation.
Whenever I deal with unknowns, I like to suppose everything is positive. Then, algebra will take care of the signs by itself. For that reason, I'll solve it using the vectorial product. All the angular velocities (the yellow, green, and red gears and the carrier) are assumed positive. Later, the cross product makes the sign appear.

For simplicity, I'll reorient the problem so we don't need to decompose the problem in two directions in the initial instant because the velocities of the interest points B and D will be exclusively in the vertical direction $y$.

Note 1: Vectors coming in and out of the screen are drawn following the standard "arrow" view. Whether you view the tip when it points to you (the dot) or the feathers (the cross) if it's the opposite. Coming out of the screen, pointing to you, will be considered the positive $z$.

Note 2: Vector $\overrightarrow{r}_{BA}$ is the vector that goes from A to B. Therefore, $\overrightarrow{r}_{BA} = - \overrightarrow{r}_{AB}$.

The rotations are:

• Yellow gear around A: $\overrightarrow{\omega}_{yA}=(0,0,\omega_{yA})\rightarrow \overrightarrow{\omega}_{y}=(0,0,\omega_{y})$
• Green gear around C: $\overrightarrow{\omega}_{gC}=(0,0,\omega_{gC})\rightarrow \overrightarrow{\omega}_{g}=(0,0,\omega_{g})$
• Red gear around E: $\overrightarrow{\omega}_{rE}=(0,0,\omega_{rE})\rightarrow \overrightarrow{\omega}_{r}=(0,0,\omega_{r})$
• Green gear around A (same as the transparent carrier): $\overrightarrow{\omega}_{gA}=\overrightarrow{\omega}_{tA}=(0,0,\omega_{tA})\rightarrow \overrightarrow{\omega}_{t}=(0,0,\omega_{t})$
• Red gear around A (same as the transparent carrier): $\overrightarrow{\omega}_{rA}=\overrightarrow{\omega}_{tA}=(0,0,\omega_{tA})\rightarrow \overrightarrow{\omega}_{t}=(0,0,\omega_{t})$

As previously mentioned, no slipping means that, at the contact point, the velocity is the same for the bodies involved. I will define the velocity of point B as part of the yellow gear $(\overrightarrow{v}_{By})$ and point B as part of the green gear $(\overrightarrow{v}_{Bg})$.
The point B in the yellow gear just moves due to the rotation of the yellow gear around A.
$$\overrightarrow{v}_{By}=\overrightarrow{\omega}_{y} \times \overrightarrow{r}_{BA} \tag{1}$$
The point B in the green gear moves due to the rotation of the green gear around its center and the displacement of the green gear around the yellow gear which corresponds to the rotation of the carrier $(\overrightarrow{\omega}_{gA}=\overrightarrow{\omega}_{t})$.
$$\overrightarrow{v}_{Bg}=\overrightarrow{\omega}_{g} \times \overrightarrow{r}_{BC}+\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{BA}+\overrightarrow{r}_{CB})\tag{2}$$
Lastly, imposing no slipping at B.
$$\overrightarrow{v}_{By}=\overrightarrow{v}_{Bg} \rightarrow \overrightarrow{\omega}_{y} \times \overrightarrow{r}_{BA} = \overrightarrow{\omega}_{g} \times \overrightarrow{r}_{BC}+\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{BA}+\overrightarrow{r}_{CB}) \tag{3}$$
Notice how in $(1)$, $(2)$ and $(3)$ I assumed positive angular velocities. The correct sign will be given by the cross-product. Also, notice that those distances correspond to the known radius of the different gears.
I will solve the cross-product at that instant where the horizontal component $x$ will be 0. I won't add more subindices to indicate we're talking about the $y$ direction because it's irrelevant. The equations will hold true for the reduction ratio no matter the orientation. I will also add the information regarding the radius of the gears instead of using the subindices that mention the points.
$$\overrightarrow{v}_{By}=\overrightarrow{v}_{Bg} \rightarrow v_{By}=v_{Bg} \rightarrow
\omega_yr_y=-\omega_gr_g+\omega_t(r_y+r_g) \tag{4}$$
Notice how $(4)$ is the same as previously derived. (You'd need to solve for the variable $\omega_y$. Remember that the angular speed, the radius, and the number of teeth are all linearly linked so you can substitute them.

Considering the green gear is the sun and the yellow gear is its planet connected by the transparent carrier.
$$\theta_y = \theta_t + \frac{d_{g}}{d_y}\theta_t - \frac{d_{g}}{d_y}\theta_g \tag{1}$$

I will do the same for the point D.
Point D in the green gear has a similar movement to point B where the only changes will be in the distance vectors.
$$\overrightarrow{v}_{Dg}=\overrightarrow{\omega}_{g} \times \overrightarrow{r}_{DC}+\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{BA}+\overrightarrow{r}_{CB})\tag{5}$$
Point D in the red gear is similar to the previous one.
$$\overrightarrow{v}_{Dr}=\overrightarrow{\omega}_{r} \times \overrightarrow{r}_{DE}+\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{BA}+2\overrightarrow{r}_{CB}+\overrightarrow{r}_{ED})\tag{6}$$
Again, solving the cross-product to get a scalar equation.
$$\overrightarrow{v}_{Dg}=\overrightarrow{v}_{Dr} \rightarrow v_{Dg}=v_{Dr} \rightarrow
\omega_gr_g+\omega_t(r_y+r_g)=-\omega_rr_r+\omega_t(r_y+2r_g+r_r) \tag{7}$$
Notice how $(7)$ is the same as previously derived. (You'd need to solve for the variable $\omega_t$. Remember that the angular speed, the radius, and the number of teeth are all linearly linked so you can substitute them.

Knowing the carrier is the same in both equations, I'll obtain the carrier's angle from the second equation to plug it into the first one.
$$\theta_t = \frac{\theta_r+\frac{d_g}{d_r}\theta_g}{1+\frac{d_g}{d_r}} = \frac{d_r\theta_r+d_g\theta_g}{d_r+d_g} \tag{3}$$

In conclusion, this method provides a systematic (although maybe tedious) way to solve these kinds of mechanisms. My confidence in it is high since I obtained the same results.
I will try to apply it to the original mechanism from the OP without as much explanation since this is the reference post to understand the method.

 

[Juanda]

I will try to apply it to the original mechanism from the OP without as much explanation since this is the reference post to understand the method.

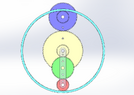
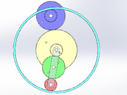
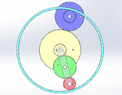
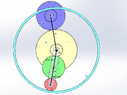
I marked the contact points in orange and the centers of rotation in grey.
For each contact point, we'll need a non-slip equation.
Notice how the rotation of the green and red gears around D is the same as the rotation of the transparent carrier. However, that's not the case for the blue gear.
I will keep talking about the gears with the same subindices as in a previous post.

There are 6 bodies. From top to bottom, they are:

1. Cyan gear $\theta_c$, $d_c$
2. Blue gear $\theta_b$, $d_b$
   • Big diameter $d_{bb}$ (EDIT: added)
   • Small diameter $d_{bs}$ (EDIT: added)
3. Yellow gear $\theta_y$
   • Big diameter $d_{yb}$
   • Small diameter $d_{ys}$
4. Transparent carrier $\theta_t$, $d_t$
5. Green gear $\theta_g$, $d_g$
6. Red gear $\theta_r$, $d_r$

In the previous example, the cross-product resulted in only one component in the vertical direction. Here, it's in the horizontal direction.
If the gears were at an arbitrary position where it's necessary to decompose the velocity in the horizontal and vertical direction, since you only care about the gear ratio, I'm fairly sure you could rotate your axis in the positive direction so you only have one component again and follow the same procedure as previously explained. Either that or solve the trigonometric system of equations resulting from the cross product. I haven't tried that though so it's only a hypothesis.

Point E
$$\overrightarrow{v}_{Ey}=\overrightarrow{\omega}_{y} \times \overrightarrow{r}_{ED} \rightarrow v_{Ey}= \omega_{y} r_{ys} \tag{1}$$
$$\overrightarrow{v}_{Eg}=\overrightarrow{\omega}_{g} \times \overrightarrow{r}_{EF}+
\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{ED}+\overrightarrow{r}_{FE})
\rightarrow
v_{Eg} = -\omega_{g} r_g + \omega_{t} (r_{ys}+r_g) \tag{2}$$
$$v_{Ey}=v_{Eg} \rightarrow \omega_{y} r_{ys} = -\omega_{g} r_g + \omega_{t} (r_{ys}+r_g) \tag{3}$$

Point G
$$\overrightarrow{v}_{Gg}=
\overrightarrow{\omega}_{g} \times \overrightarrow{r}_{GF}
+
\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{ED} + \overrightarrow{r}_{FE})
\rightarrow
v_{Gg} = \omega_{g} r_g +\omega_{t} (r_{ys} + r_g)
\tag{4}$$
$$\overrightarrow{v}_{Gr}=
\overrightarrow{\omega}_{r} \times \overrightarrow{r}_{GH}
+
\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{ED}+2\overrightarrow{r}_{FE}+\overrightarrow{r}_{HG})
\rightarrow
{v}_{Gr}=-\omega_r r_r + \omega_t (r_{ys}+2r_g+r_r)
\tag{5}$$
$$v_{Gg}=v_{Gr} \rightarrow \omega_{g} r_g +\omega_{t} (r_{ys} + r_g) = -\omega_r r_r + \omega_t (r_{ys}+2r_g+r_r)\tag{6}$$

Point I
$$\overrightarrow{v}_{Ir}=
\overrightarrow{\omega}_{r} \times \overrightarrow{r}_{IH}
+
\overrightarrow{\omega}_{t} \times (\overrightarrow{r}_{ED} + 2\overrightarrow{r}_{FE} + \overrightarrow{r}_{HG})
\rightarrow
v_{Ir} = \omega_{r} r_r +\omega_{t} (r_{ys} + 2r_g + r_r)
\tag{7}$$
$$\overrightarrow{v}_{Ic}=
\overrightarrow{\omega}_{c} \times (\overrightarrow{r}_{ED} + 2\overrightarrow{r}_{FE} + 2\overrightarrow{r}_{HG})
\rightarrow
v_{Ic}= \omega_{c} r_{c} \tag{8}$$
$$v_{Ir}=v_{Ic} \rightarrow \omega_{r} r_r +\omega_{t} (r_{ys} + 2r_g + r_r) = \omega_{c} r_{c}\tag{9}$$

Point C
$$\overrightarrow{v}_{Cy}=
\overrightarrow{\omega}_{y} \times \overrightarrow{r}_{CD}
\rightarrow
v_{Cy}= -\omega_{y} r_{yb} \tag{10}$$
$$\overrightarrow{v}_{Cb}=
\overrightarrow{\omega}_{b} \times \overrightarrow{r}_{CB}+
\overrightarrow{\omega}_{bD} \times (\overrightarrow{r}_{CD}+\overrightarrow{r}_{BC})
\rightarrow
v_{Cb} = \omega_{b} r_{bb} - \omega_{bD} (r_{yb}+r_{bb}) \tag{11}$$
Notice that in $(11)$ I had to introduce the rotation of the blue gear around the point D $(\omega_{bD})$. Here there is no carrier so that new variable is necessary.
$$v_{Cy}=v_{Cb}\rightarrow -\omega_{y} r_{yb} = \omega_{b} r_{bb} - \omega_{bD} (r_{yb}+r_{bb}) \tag{12}$$

Point A
$$\overrightarrow{v}_{Ab}=
\overrightarrow{\omega}_{b} \times \overrightarrow{r}_{AB}
+
\overrightarrow{\omega}_{bD} \times (\overrightarrow{r}_{CD} + \overrightarrow{r}_{BC})
\rightarrow
v_{Ab} = -\omega_{b} r_{bs} - \omega_{bD} (r_{yb} + r_{bb})
\tag{13}$$
$$\overrightarrow{v}_{Ac}=\overrightarrow{\omega}_{c} \times (\overrightarrow{r}_{CD}+\overrightarrow{r}_{BC}+\overrightarrow{r}_{AB})
\rightarrow
{v}_{Ac}=-{\omega}_{b} {r}_{c} \tag{14}$$
$$v_{Ab}=v_{Ac} \rightarrow -\omega_{b} r_{bs} - \omega_{bD} (r_{yb} + r_{bb}) = -{\omega}_{b} {r}_{c} \tag{15}$$


That's all. Way longer than I expected. Repetitive tasks like this are for computers. I would be surprised if I didn't introduce some typo as my eyes got tired.

The point is that with the equations $(3)$, $(6)$, $(9)$, $(12)$ and $(15)$ everything should be defined.
I didn't end up using the paper you provided but I'm fairly confident about this result. Let me know if you find any errors.

 

[PlanetaryGearbox]

Hello @Juanda thank you sooo much for these calculations!

I tried equations 3, 6, 9 for the yellow, green, red, cyan (ring) gears and it worked perfectly, with the numbers and the direction of movements of gears too! I'll be honest, I don't quite understand them immediately, but I will definitely study what you wrote to get an understanding of how you arrived at the end, because even though I got the results for the compound planetary gear (blue gear) and its carrier from the link, I still wasn't able to figure out the calculations for the red gear and its carrier, but thanks to your kind genius you derived the formulae which work pefectly.

Also, it's my fault that I didn't show in the CAD, but there is a carrier between yellow and dark blue gear too. I have shown another picture with the exact measurements of everything, and the black lines represent carriers.

Again, I cannot thank you enough for taking such a long time to not only derive these equations but type them out so beautifully and painstakingly too! Thank you so much. I wish you nothing but the best in your career and life.

 

[Juanda]

Hello @Juanda thank you sooo much for these calculations!

I tried equations 3, 6, 9 for the yellow, green, red, cyan (ring) gears and it worked perfectly, with the numbers and the direction of movements of gears too! I'll be honest, I don't quite understand them immediately, but I will definitely study what you wrote to get an understanding of how you arrived at the end, because even though I got the results for the compound planetary gear (blue gear) and its carrier from the link, I still wasn't able to figure out the calculations for the red gear and its carrier, but thanks to your kind genius you derived the formulae which work pefectly.

I'm glad it helped. I didn't see it clearly in the beginning so I got it wrong in the first posts but it was fun to revisit this topic. Mechanical joints can be complicated to derive but, once a step-by-step methodology is implemented the pieces fall in place. That's why I tried to fall back to a simpler case to get the math right and then build from there.
That method often works for me no matter the topic. Start simple, go complex as you get more capable.
If you have trouble understanding the method I'd recommend focusing on post #10 before moving on to your planetary gearbox. If you have some specific questions about those posts I could try to help you.

Also, it's my fault that I didn't show in the CAD, but there is a carrier between yellow and dark blue gear too. I have shown another picture with the exact measurements of everything, and the black lines represent carriers.

Again, I cannot thank you enough for taking such a long time to not only derive these equations but type them out so beautifully and painstakingly too! Thank you so much. I wish you nothing but the best in your career and life.

The equations regarding the blue gear will change then as specified in the formulas for point C.

Point C
$$\overrightarrow{v}_{Cy}=
\overrightarrow{\omega}_{y} \times \overrightarrow{r}_{CD}
\rightarrow
v_{Cy}= -\omega_{y} r_{yb} \tag{10}$$
$$\overrightarrow{v}_{Cb}=
\overrightarrow{\omega}_{b} \times \overrightarrow{r}_{CB}+
\overrightarrow{\omega}_{bD} \times (\overrightarrow{r}_{CD}+\overrightarrow{r}_{BC})
\rightarrow
v_{Cb} = \omega_{b} r_{bb} - \omega_{bD} (r_{yb}+r_{bb}) \tag{11}$$
Notice that in $(11)$ I had to introduce the rotation of the blue gear around the point D $(\omega_{bD})$. Here there is no carrier so that new variable is necessary.
$$v_{Cy}=v_{Cb}\rightarrow -\omega_{y} r_{yb} = \omega_{b} r_{bb} - \omega_{bD} (r_{yb}+r_{bb}) \tag{12}$$

Once you learn the method you should be able to correct the formulas to include the influence of the carrier yourself. It'd be a good exercise to make sure you got it.

 

[PlanetaryGearbox]

I'm glad it helped. I didn't see it clearly in the beginning so I got it wrong in the first posts but it was fun to revisit this topic. Mechanical joints can be complicated to derive but, once a step-by-step methodology is implemented the pieces fall in place. That's why I tried to fall back to a simpler case to get the math right and then build from there.
That method often works for me no matter the topic. Start simple, go complex as you get more capable.
If you have trouble understanding the method I'd recommend focusing on post #10 before moving on to your planetary gearbox. If you have some specific questions about those posts I could try to help you.



The equations regarding the blue gear will change then as specified in the formulas for point C.

Once you learn the method you should be able to correct the formulas to include the influence of the carrier yourself. It'd be a good exercise to make sure you got it.

You are absolutely right about starting from basics. In fact, I was trying to do exactly that when I saw the derivation of Willi's equation, but I got too caught up with their method of adding angles. I read your last two posts in a lot more detail and now I truly understand everything and can solve for the carrier on my own now. Thank you, thank you so much for your help. These calculations wouldn't have been possible without you, and I say this because I truly didn't expect someone to help me with the effort and sincerity with which you did.

 

[Juanda]

You are absolutely right about starting from basics. In fact, I was trying to do exactly that when I saw the derivation of Willi's equation, but I got too caught up with their method of adding angles. I read your last two posts in a lot more detail and now I truly understand everything and can solve for the carrier on my own now. Thank you, thank you so much for your help. These calculations wouldn't have been possible without you, and I say this because I truly didn't expect someone to help me with the effort and sincerity with which you did.

So far I have often found a very constructive mentality in Physics Forums. There are several people looking forward to learning and teaching in many posts.
Who knows, maybe you can find some posts in which to contribute to helping other troubled guys like you were a few days ago.

 

[PlanetaryGearbox]

So far I have often found a very constructive mentality in Physics Forums. There are several people looking forward to learning and teaching in many posts.
Who knows, maybe you can find some posts in which to contribute to helping other troubled guys like you were a few days ago.

Yes! I look forward to participating more, although maybe not from this account as it's tied to my work. Thanks though, for everything!