How to check chaotic system using Lyapunov

[ohaited]

Greetings!

Hey, can anyone help me? I need an explanation how can Lyapunov help me to check the system weather it is chaotic or not. Let say I have this equation Rossler System Eq.(1)

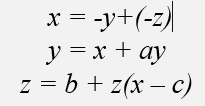
So how can you tell that the system have chaotic behavior or not? Does it depends on parameters? or from initial constant (a,b,c)? A general and specific clarification is needed. Because I have this paper research that talk about Rossler System Eq. (1) can have chaotic behavior when the initial a=b=0.2 and c= 5.7

Thanks, your consideration is appreciated!

 

[jim mcnamara]

Could you please tell us the title of the paper and where/when it was published? It might help a lot to give you the best answer.

 

[ohaited]

Could you please tell us the title of the paper and where/when it was published? It might help a lot to give you the best answer.

Hey there, sorry for not attaching the paper with my question. So here it is: Paper

 

[Filip Larsen]

So how can you tell that the system have chaotic behavior or not? Does it depends on parameters? or from initial constant (a,b,c)?

In short you can determine if a particular system is chaotic by solving the differential equations numerically and calculate the Lyapunov exponents along the (non-transient) trajectory. If there is at least one positive Lyapunov exponent then the trajectory is chaotic and hence the system for its given parameters and initial state is considered chaotic.

For a practical guide on how to calculate it you may be inspired by the description on http://sprott.physics.wisc.edu/chaos/lyapexp.htm. Way back at university I used Practical Numerical Algorithms for Chaotic Systems by Parker and Chua, but that is a bit old now (but most likely still relevant).